Hao (Howard) Wang
University of Alberta
Cognitive Movement Modelling and Analysis
Friday, December 12, 2025, 2:00pm
Online
Abstract: Based on our recent efforts in spatial memory modelling and analysis for cognitive animal movement, I will briefly review this topic and mention challenges in modelling and rigorous analysis. Some showcases will be given as idea illustrations.
Rick Miranda
Professor of Mathematics
Vice Chancellor for Collaboration & Integration, CSU System
Colorado State University
Variations on Pascal's Theorem
Friday, October 17, 2025, 4:30pm
Ungar Room 506
Abstract: Given a hexagon inscribed in an ellipse, the three intersection points of opposite sides of the hexagon are (miraculously!) collinear. I'll review this famous theorem, give a new relatively recent proof, and discuss a generalization to higher dimensions that has a similar character.
Morgan Brown
University of Miami
Symmetry and the Logic of Irreversibility
Thursday, April 24, 2025, 5:00pm
Ungar Room 402
Abstract: I will describe a formalism for quantum theory in which the free energy carried by a particle is certified by its symmetry under a very large finite cyclic group. This allows the semantic resource of information to be identified internally in the theory. One benefit of this formalism is that this symmetry creates superselection rules which forbid observations in non-classical states. A second benefit is that adjusting the symmetry group via a finite quotient can create either a change of scale or a loss of the internal information allowing us to model irreversible processes.
Eric Mazur
Harvard University
University of Miami
Ilene M. Dresner Distinguished Visiting Scholar
Confessions of a Converted Lecturer
Monday, April 7, 2025, 1:30pm
Ungar Room 411
Abstract: I once thought I was a good teacher–until I realized my students were simply memorizing material rather than truly understanding it. The question was: who was to blame? The students? The content?
In this talk, I'll share how I came to the painful realization that the real culprit was my teaching approach. I'll also demonstrate how I've adjusted my methods to improve student engagement and performance.
Svetlana Roudenko
Florida International University
Bi-harmonic Nonlinear Schrödinger Equation:
Well-posedness and Solitary Waves
Tuesday, March 18, 2025, 5:00pm
Ungar Room 402
Abstract: The bi-harmonic nonlinear Schrödinger (NLS) equation (with the double Laplacian or quartic dispersion) has recently reappeared in physics as pure quartic solitons have been experimentally obtained. However, a mathematical theory, including well-posedness, is still not adequately addressed; nor does there exist a satisfactory understanding of soliton theory in this context. In the first part of the talk, we discuss the local well-posedness, using an approach that avoids the standard method via Strichartz estimates. Then we look at a more global behavior of solutions, in particular, ground state or soliton solutions and discuss their stability and global dynamics, which turns out to be much richer than in the standard NLS case.
Alexander V. Turbiner
Universidad Nacional Autónoma de México (UNAM)
Stony Brook University
3-body Elliptic Calogero Model (equivalently 2D-Lamé Equation):
A Solution
Thursday, February 6, 2025, 5:00pm
Ungar Room 402
Abstract: Lamé equation (operator) (Lamé, 1837) is one of the most fundamental objects in ODE and quantum mechanics. After its introduction and a brief review of the main properties (algebraic form, rational form, sl(2) Lie algebraic structure, equivalent the Euler-Arnold quantum top, polynomial eigenfunctions) two 2-dimensional generalizations are considered: BC2 elliptic model and highly-non-trivial A2 elliptic 3-body (Calogero) model. Non-trivial change of variables leading to algebraic differential operators (with polynomial coefficients) is introduced. Both models have the same hidden sl(3)-algebraic structure and they are equivalent to the sl(3) Euler-Arnold quantum top in a constant magnetic field. For special discrete values of parameters (coupling constants) the resulting operators possess finite-dimensional invariant subspace and admit polynomial eigenfunctions. The invariant subspace coincides with representation space of the algebra sl(3).
Marcel Nutz
Columbia University
Entropic Selection in Optimal Transport
Friday, January 17, 2025, 4:00pm
Ungar Room 402
Abstract: Optimal transport is widely used to quantify the distance between two probability distributions or data sets. The optimal transport problem can admit many solutions, for instance when the cost function is the Euclidean distance on Rd (Monge's problem). On the other hand, entropically regularized optimal transport (EOT) always has a unique optimizer. It is a longstanding open problem whether EOT selects some particular optimal transport coupling in the vanishing regularization limit, and what that coupling would look like. We provide a surprising answer for Monge's problem in dimension d > 1.
This is ongoing work with Chenyang Zhong.
Ugur G. Abdulla
Okinawa Institute of Science and Technology
Removability of the Fundamental Singularity for the Heat Equation and its Measure-theoretical, Topological and Probabilistic Consequences
Wednesday, November 20, 2024, 5:30pm
Ungar Room 402
Abstract: The major problem in the Analysis of PDEs is understanding the nature of singularities of solutions to the PDEs reflecting the natural phenomena. In this talk, I will present new Wiener-type criteria for the removability of the fundamental singularity for the parabolic PDEs. The criteria characterize the uniqueness of boundary value problems with singular data, reveal the nature of the parabolic measure of the singularity point, asymptotic laws for the conditional Markov processes, and criteria for thinness in minimal-fine topology. The talk will be oriented to a general audience including non-expert faculty and graduate students.
Jane Heffernan
York University, Toronto, Canada
Multi-Scale Modelling: Immunity
Tuesday, November 5, 2024, 5:00pm
Ungar Room 402
Abstract: Immunity is both presented as a characteristic of an individual, and of a population. Immunity is generated in individuals through vaccination and/or infection, and it is quantified in populations to determine If herd immunity (or a specific level of wanted immunity in the population) can be achieved or maintained. In this talk we will provide an overview of models of immunity at both scales. Mathematical models of antibody and memory cell generation, maintenance, and waning (decay) in-host will be introduced as well as epidemiological models with detailed immunity distributions. The dynamics of COVID-19, measles and influenza immunity generation and decay from vaccination and infection in individuals and populations will be highlighted.
Yasuhuro Takeuchi
Aoyama Gakuin University, Japan
Bifurcation Analysis in a Tumor-Immune System Interaction Model
Thursday, September 26, 2024, 5:00pm
Ungar Room 402
Abstract: We study a tumor-immune system interaction model with dendritic cell therapy and immune response delay. Our results reveal that the delay can destabilize the stable positive equilibrium through Hopf bifurcation. Furthermore, the direction and stability of Hopf bifurcation are derived. When there is a cusp, we show that it is a BT singularity for any delay and the delay model also undergoes BT bifurcation. Finally, numerical simulations are presented to illustrate the theoretical results.
References:
1. Dynamical behavior of combinational immune boost against tumor, M. Nagata, Y. Furuta, Y. Takeuchi and S. Nakaoka, Japan J. Ind. App. Math., Vol.32, No.3, 2015, 759-770.
2. Mathematical modeling and analysis of combinational immune boost for tumor elimination, N. Nakada, M. Nagata, Y. Takeuchi, and S. Nakaoka, Citation: AIP Conference Proceedings 1723, 2016, 020002.
3. Bifurcation analysis in a tumor-immune system interaction model with dendritic cell therapy and immune response delay, Y. Zhang, L. Xie, Y. Dong, J. Huang, S. Ruan, and Y. Takeuchi, SIAM Journal on Applied Mathematics, SIAM J Appl. Math., Vol. 83, No.5, 2023, 1892-1914.
Ruobing Zhang
Princeton University
Metric Geometry of Einstein Manifolds and Generalizations
Monday, May 6, 2024, 5:00pm
Ungar Room 402
Abstract: This lecture concerns the metric Riemannian geometry of Einstein manifolds. We will exhibit the rich geometric/topological structures of Einstein manifolds and specifically focus on the structure theory of moduli spaces of Einstein metrics. My recent works center around the intriguing problems regarding the compactification of the moduli space of Einstein metrics, which tells us how Einstein manifolds can degenerate. We will introduce recent major progress and propose several open questions in the field.
Rafal Komendarczyk
Tulane University
Linking and Knotting in Volume Preserving Flows
Thursday, March 28, 2024, 5:00pm
Ungar Room 402
Abstract: The topology of orbits in volume-preserving flows is of special interest in the areas of fluid dynamics and plasma physics. The well-known helicity invariant, which measures an asymptotic average linking number of the orbits of the flow, provides an estimate for the 𝐿²-energy of the field. Invariants of flows, derived from various knot and link invariants, are of special interest and have been studied extensively by researchers. In this talk, I will present an overview of the subject and its connections to other areas of low-dimensional topology and geometry.
Philip Hanlon
Distinguished Presidential Scholar, University of Miami
President Emeritus, Dartmouth College
The Amazing Eulerian Idempotents
Monday, March 18, 2024, 5:00pm
Ungar Room 402
Abstract: The Eulerian idempotents, sitting inside the group algebra of the symmetric group, are a set of pairwise orthogonal idempotents that sum to the identity. They are remarkable for the broad range of contexts within which they arise, from homological algebra to card shuffling to chromatic polynomials of graphs. In this lecture, we will introduce the Eulerian idempotents, discuss some of their algebraic properties and survey some of their many applications.
Lisa Fauci
Pendergraft Nola Lee Haynes Professor, Tulane University
2023 Inductee to the National Academy of Sciences
Modeling Choices in the Biofluids of Locomotion:
Two Case Studies
Friday, March 8, 2024, 5:00pm
Ungar Room 402
Abstract: At the macroscale, the undulatory swimming gait of a fish emerges from the coupling of neural signaling, passive body properties and muscle mechanics with the surrounding fluid environment. At the microscale, unicellular and colonial protists use flagella to swim and to create a water current transporting bacterial prey for capture. These are two examples of systems in biological fluid dynamics that we have modeled in collaboration with experimentalists. We will discuss the choices made in model development and the computational frameworks used. In particular, will discuss coordinated laboratory experiments and simulations that investigate the swimming and feeding performance of individual choanoflagellates carrying bacterial prey, as well the hydrodynamic performance of colonies of hundreds of these cells. At the macroscale, we will present a closed-loop model that examines the hypothesis that amplified body-sensing feedback could restore effective locomotion in lampreys with spinal injuries.
This talk is based on joint works with F. Delarue, M. Shkolnikov, X. Zhang and Y. Guo.
Sergey Nadtochiy
Illinois Institute of Technology
Physical Solution to Stefan Equation
Friday, March 1, 2024, 3:00pm
Ungar Room 402
Abstract: This talk is concerned with the probabilistic methods for solving Stefan free-boundary PDEs. The latter equations appear in many models of fundamental physical and biological processes, such as: phase transition (i.e., melting/freezing), phase segregation (e.g., aging of alloys), crystal growth, interaction among neurons, etc. Despite their importance, to date, there exists no general existence and uniqueness theory for such equations due to the potential singularity of the solutions. Recently, the probabilistic methods, based on the analysis of associated mean-field particle systems and McKean-Vlasov equations, were successfully used to tackle the mathematical challenges that could not be addressed by the classical analytic methods, yielding the notion a physical solution of Stefan equation and its well-posedness. I will present an overview of the existing results, including the recently obtained proof of well-posedness of Stefan equation with surface tension under radial symmetry.
This talk is based on joint works with F. Delarue, M. Shkolnikov, X. Zhang and Y. Guo.
Eran Nevo
Einstein Institute of Mathematics
Hebrew University Jerusalem
Rigidity, Expansion and Polytopes
Thursday, February 29, 2024, 5:00pm
Ungar Room 402
Abstract: Given a graph G and an embedding of its vertices in Rd, what continuous motions of the vertices preserve all edge lengths? Clearly all motions induced by an isometry of Rd do, these are the trivial motions; are there any others? If the answer is NO for all (equivalently, for one) generic embedding, G is called d-rigid. What are the d-rigid graphs? This problem has been extensively studied since the 70s, and is still widely open for d≥3. It is studied mainly from algebraic geometry and combinatorial points of view. Variants of it, especially in dimensions 2 and 3, are of importance also beyond mathematics, e.g. in structural engineering, computational biology and more.
I will focus on a quantitative version of rigidity via spectral analysis of the related stiffness matrix, including the construction of "rigidity expanders", generalizing expander graphs. Higher dimensional notions of rigidity and stiffness matrices, and their relation to the study of polytopes, will be addressed too.
Lionel Levine
Cornell University
Math for AI Safety
Monday, February 19, 2024, 5:00pm
Ungar Room 402
Abstract: AI holds great promise and, many believe, great peril. What can mathematicians contribute to ensuring that promise is fulfilled, and peril avoided? I'll highlight research directions relevant to AI safety in many different fields of math. I'll also touch on the question of how educators can empower students to succeed in a world pervaded by AI, and to shape that world for the better: After all, many of today's math majors will be tomorrow's AI engineers. This talk will be interactive, and I'll mostly supply questions rather than answers, so please come prepared to debate!
Karola Mészáros
Cornell University
Log-concavity of the Alexander Polynomial
Friday, February 16, 2024, 5:00pm
Ungar Room 402
Abstract: The central question of knot theory is that of distinguishing links up to isotopy. The first polynomial invariant of links devised to help answer this question was the Alexander polynomial (1928). Almost a century after its introduction, it still presents us with tantalizing questions, such as Fox's conjecture (1962) that the absolute values of the coefficients of the Alexander polynomial ΔL(t) of an alternating link L are unimodal. Fox's conjecture remains open in general with special cases settled by Hartley (1979) for two-bridge knots, by Murasugi (1985) for a family of alternating algebraic links, and by Ozsváth and Szabó (2003) for the case of genus 2 alternating knots, among others. We settle Fox's conjecture for special alternating links. We do so by proving that a certain multivariate generalization of the Alexander polynomial of special alternating links is Lorentzian. As a consequence, we obtain that the absolute values of the coefficients of ΔL(t), where L is a special alternating link, form a log-concave sequence with no internal zeros. In particular, they are unimodal. This talk is based on joint work with Elena Hafner and Alexander Vidinas.
Benjamin Braun
University of Kentucky
Ehrhart Theory and Lattice Simplices
Thursday, November 9, 2023, 5:00pm
Ungar Room 402
Abstract: The Ehrhart h*-polynomial of a lattice polytope is an important and well-studied invariant in geometric and algebraic combinatorics. However, many fundamental questions regarding these polynomials remain unanswered. For lattice simplices, the h*-polynomial reflects both arithmetic and geometric structure, and these objects form a surprisingly rich family of polytopes from an Ehrhart-theoretic perspective. In this talk, I will provide a survey of examples, theorems, and questions regarding both h*-polynomials and local h*-polynomials for lattice simplices.
Marcelo Disconzi
Vanderbilt University
General-relativistic Viscous Fluids
Thursday, October 19, 2023, 5:00pm
Ungar Room 402
Abstract: In this talk, we will review some recent developments at the intersection of mathematics and physics regarding theories of relativistic fluids with viscosity. The discovery of the quark-gluon plasma that forms in heavy-ion collision experiments provides a unique opportunity to study properties of matter under extreme conditions, as the quark-gluon plasma is the hottest, smallest, and densest fluid known to humanity. Studying the quark-gluon plasma also provides a window into the earliest moments of the universe, since microseconds after the Big Bang the universe was filled with matter in the form of the quark-gluon plasma.
For more than two decades, the community has intensely studied the quark-gluon plasma with the help of a rich interaction of experiments, theory, phenomenology, and numerical simulations. From these investigations, a coherent picture has emerged, indicating that the quark-gluon plasma behaves essentially like a relativistic liquid with viscosity.
More recently, state-of-the-art numerical simulations strongly suggested that viscous and dissipative effects can also have non-negligible effects on gravitational waves produced by binary neutron star mergers. But despite the importance of viscous effects for the study of such systems, a robust and mathematically sound theory of relativistic fluids with viscosity is still lacking. This is due, in part, to difficulties in preserving causality upon the inclusion of viscous and dissipative effects into theories of relativistic fluids.
In this talk, we will survey the history of the problem and report on a new approach to relativistic viscous fluids that addresses these issues. This talk is intended for a general Math and Physics audience.
Juhi Jang
University of Southern California
Dynamics of Gaseous Stars
Wednesday, October 11, 2023, 5:00pm
Ungar Room 402
Abstract: In astrophysical fluid dynamics, stars are considered as isolated fluid masses subject to self-gravity. A classical model of a self-gravitating Newtonian star is given by the gravitational Euler- Poisson system, while a relativistic star is modeled by the Einstein-Euler system. In the talk, I will review some recent progress on the local and global dynamics of Newtonian star solutions, and discuss mathematical construction of self-similar gravitational collapse of Newtonian stars including Larson-Penston solution for the isothermal stars, Yahil solution for polytropic stars, which show the existence of smooth initial data that lead to finite time collapse, characterized by the blow-up of the star density. If time permits, I will also discuss the relativistic analogue of Larson-Penston solutions and formation of naked singularities for the Einstein-Euler system.
Igor Pak
University of California, Los Angeles
Combinatorial Inequalities
Monday, May 1, 2023, 5:00pm
Ungar Room 402
Abstract: In the ocean of combinatorial inequalities, two islands are especially difficult. First, Mason's conjectures say that the number of forests in a graph with k edges is log-concave. More generally, the number of independent sets of size k in a matroid is log-concave. These results were established just recently, in a remarkable series of papers by Huh and others, inspired by algebro-geometric considerations.
Second, Stanley's inequality for the numbers of linear extensions of a poset with value k at a given poset element, is log-concave. This was originally conjectured by Chung, Fishburn and Graham, and famously proved by Stanley in 1981 using the Alexandrov–Fenchel inequalities in convex geometry.
In the first part of the talk we will survey these and other combinatorial inequalities. I will then briefly discuss our new framework of combinatorial atlas which allows one to give elementary proofs of the two results above, and extend them in several directions. The talk is aimed at the general audience.
Christos Mantoulidis
Rice University
Generic Regularity of Minimizing Hypersurfaces in Dimensions Up to 10
Thursday, April 27, 2023, 5:00pm
Ungar Room 402
Abstract: A classical problem in geometric analysis and the calculus of variations is to find least-area submanifolds spanning a prescribed boundary. Deep results in geometric measure theory developed between the 1950s and the 1970s guarantee that for every smooth compact (n-2)-dimensional submanifold L in R^n there exists a smooth compact hypersurface-with-boundary that spans L with least area – provided n <= 7. When n >= 8, some boundaries L do not bound smooth least-area hypersurfaces. In this talk, I will discuss recent joint work with O. Chodosh and F. Schulze where we prove that the non-existence of smooth minimizers is Baire non-generic if n <= 10. This improves upon the analogous 1980's result for n=8 by R. Hardt and L. Simon.
Jianhong Wu
York University, Canada
Global and Generic Dynamics of Nonlinear Systems with Embedded Predator-Prey Feedback Cycles
Tuesday, April 25, 2023, 5:00pm
Ungar Room 402
Abstract: Many nonlinear systems with embedded predator-prey interactions have the order-preserving monotonicity with respect to a rank-k cone (with k>1). We show such systems enjoy the limit-set trichotomy properties (including potential heteroclinic cycles), and the restricted semiflow on any given omega-set can be characterized by a Lipschitz-continuous flow on the k-dimensional Euclidean space. In the case where k=2, we can also obtain the generic Poincare-Bendixson theorem, and this can be used to establish the generic periodicity of high-dimensional epidemic systems with non-standard nonlinear instance functions. The talk is based on a series of studies in collaboration with Lirui Feng and Yi Wang, some of these results have been reported in SIAM J. Math. Anal. (2017), J. Differential equations (2021) and SIAM J. Applied Math. (2022), and many more to come.
Yanyan Li
Rutgers University
Symmetry of Hypersurfaces and the Hopf Lemma
Tuesday, April 18, 2023, 5:00pm
Ungar Room 402
Abstract: A classical theorem of A.D. Alexandrov says that a connected compact smooth hypersurface in Euclidean space with constant mean curvature must be a sphere. We give exposition to results on symmetry properties of hypersurfaces with ordered mean curvature and associated variations of the Hopf Lemma. Some open problems will be discussed.
Dr. Bryna Kra
Northwestern University
Infinite Patterns in Large Sets of Integers
Friday, March 31, 2023, 5:00pm
Ungar Room 402
Abstract: Resolving a conjecture of Erdős and Turan from the 1930s, in the 1970s Szemerédi showed that a set of integers with positive upper density contains arbitrarily long arithmetic progressions. Soon thereafter, Furstenberg used Ergodic Theory to give a new proof of this result, leading to the development of combinatorial ergodic theory. These tools have led to uncovering new patterns that occur in any sufficiently large set of integers, but until recently all such patterns have been finite. Based on joint work with Joel Moreira, Florian Richter, and Donald Robertson, we discuss recent developments for infinite patterns, including the resolution of conjectures of Erdős.
Inkyung Ahn
Korea University, Korea
Population Models with Fokker-Planck-type Diffusions Incorporating Perceptual Constraints of Species in a Habitat with Spatial Heterogeneity
Tuesday, February 14, 2023, 5:00pm
Ungar 528B
Abstract: In this talk, we examine the predator-prey models in a spatially heterogeneous region where the dispersal of predators is non-uniform, a process known as prey-induced dispersal (PYID). We incorporate the perceptual constraints of species in our model and examine how PYID affects the dynamics and coexistence of the system. Our analysis is based on a Holling-type II functional response model under no-flux boundary conditions. We analyze the local stability of the semi-trivial solution in models with PID and linear dispersal in the absence of predators. Furthermore, we investigate the local and global bifurcation from the semi-trivial solution in models with two different dispersals. Our results show that if a predator's satisfaction with the prey density is higher than a certain level, it may not be beneficial in terms of their fitness. Meanwhile, if predators change their motility when they are appropriately satisfied with the amount of prey, they will obtain a survival advantage. Additionally, if time allows, we discuss competition models with starvation-driven diffusions (SDD) and perceptual constraints of species.
Dr. René Mboro
University of Miami/IMSA
On Rationality Questions for Cubic Hypersurfaces
Wednesday, May 4, 2022, 5:00pm
Ungar Room 402
Abstract: Over the past two centuries, rationality questions and especially rationality of complex cubic hypersurfaces have been one of the driving topic of the development of algebraic geometry. In this talk, we will give an overview of the state of our knowledge about the geometry of cubic hypersurfaces of dimension up to 5.
Dr. Alan Hastings
University of California at Davis
Transient Dynamics:
The Key to Ecological Understanding
Friday, April 15, 2022, 5:00pm
Ungar Room 402
Abstract: Much of classical ecological theory is focused on the long-term behavior of ecological models yet the time scales of ecological dynamics are such that a focus on asymptotic behavior is likely misguided. Ecological conclusions would likely change, but additionally much mathematical theory focuses on asymptotic behavior as well. I will begin with some of my much older work that suggests the importance of transients and some of the challenges. I will then focus on more recent work, most of which has been done with a wonderful group of colleagues from a working group that began at NIMBioS and has continued. We have given a rough classification of features that produce transients similar to approaches for understanding dynamical systems, examined implications for management, and examined transients in systems where stochasticity is important.
Dr. Alexander Volberg
Michigan State University
Hausdorff Center for Mathematics, Bonn University
Enflo's Problem and Beyond
Friday, March 25, 2022, 5:00pm
Ungar Room 402
Abstract: Harmonic analysis on Hamming cube became prominent because of its connections with theoretical computer science and, in particular, with quantum algorithms. It turns out that it is an important tool in solving some old conjectures.
Enflo's problem deals with Poincaré type inequality for functions of Rademacher random variables. The problem was solved recently by P. Ivanisvili, R. Van Handel and myself. However, this type of Poincaré inequality is only one out of the whole scale of inequalities filling the gap between Pisier's inequality and singular integral inequalities on Hamming cube. It is important and interesting a) to understand what are the sharp constants in these results b) what is the stock of Banach spaces X such that the results hold for functions of Rademacher random variables with values in X. I will explain this and the relations with the Ribe program and Bourgain's discretization theorem.
Dr. Stefan Czimek
Brown University
The Characteristic Gluing Problem of General Relativity
Monday, December 13, 2021, 11:30am
Ungar Room 402
Abstract: The Einstein equations describe the dynamics of space-time in general relativity. It is well-known that – analogous to the case of Maxwell's equations – initial data for the Einstein equations needs to satisfy constraint equations. One approach to study the rigidity and flexibility of the Einstein equations is by considering gluing problems for initial data. The so-called spacelike gluing problem for initial data on slices of constant time has been intensively studied by Riemannian geometers. In this talk I will present recent work with S. Aretakis and I. Rodnianski, where we introduce the so-called characteristic gluing problem for initial data along light cones (i.e., characteristic hypersurfaces for the Einstein equations). The characteristic gluing problem is fundamentally different from the spacelike problem and displays novel rigidity and flexibility features. We moreover show how to apply our characteristic gluing to prove gluing constructions for spacelike initial data. Towards the end of the talk, I will discuss future directions.
Dr. Zhongshan An
University of Connecticut
Geometric Boundary Conditions in General Relativity
Thursday, December 9, 2021, 5:00pm
Ungar Room 402
Abstract: In general relativity, spacetime metrics satisfy the Einstein equations, which are a system of nonlinear partial differential equations. When the spacetime has nonempty boundary, it is natural to ask what geometric boundary conditions are well-posed for the Einstein equations. The study of geometric boundary conditions not only gives rise to interesting geometric PDE problems, but also plays an important role in the study of quasi-local mass of compact spacetimes in general relativity.
In this talk we will discuss geometric boundary conditions for the vacuum Einstein equations as a hyperbolic system, and also boundary conditions for the stationary vacuum Einstein equations as an elliptic system. Then we will talk about applications of these geometric boundary value problems in the construction of quasi-local mass in general relativity.
Dr. Da Rong (Daren) Cheng
University of Waterloo
Existence of Constant Mean Curvature Surfaces
Monday, December 6, 2021, 5:00pm
Ungar Room 402
Abstract: Constant mean curvature (CMC) surfaces are two-dimensional analogues of curves with constant geodesic curvature. They originated with the work of Young, Laplace and Gauss on capillary surfaces, and have since appeared in models of many other physical phenomena. Geometrically, CMC surfaces are critical points of the area functional subject to a volume constraint. The simplicity of this variational characterization and the variety of contexts in which CMC surfaces arise makes it interesting to establish a satisfactory existence theory, the pursuit of which has been a major impetus for the development of the calculus of variations. In this talk, I'll discuss some classical results and recent developments on the variational construction of CMC surfaces.
Dr. Demetre Kazaras
Duke University
How Does Mass Affect the Geometry of Space?
Monday, November 29, 2021, 5:00pm
Ungar Room 402
Abstract: In General Relativity, the ADM mass of an isolated gravitational system is a geometric invariant measuring the total mass due to matter and other fields present in spacetime. The celebrated Positive Mass Theorem of Schoen-Yau and Witten states that this invariant is non-negative and vanishes only for flat spacetime. In recent work, we showed how to compute ADM mass in 3 spatial dimensions by studying harmonic functions. Now we will use this formula to consider the following question: How flat is an "asymptotically flat" space with very little total mass? The existence of wormholes and gravity wells make this question subtle. We make progress on this problem and partially confirm conjectures made by Huisken-Ilmanen and Lee-Sormani.
Dr. Anastasiia Tsvietkova
Rutgers University, Newark
NP-hard Problems Naturally Arising in Knot Theory
Monday, March 29, 2021, 5:00pm
Online
Abstract: Low-dimensional topology and geometry has many problems with an easy formulation, but a hard solution. Despite our intuitive feeling that these problems are "hard", lower or upper bounds on algorithmic complexity are known only for some of them. Recently, several problems that lie at the heart of classical knot theory were shown to be NP-hard, which means it is unlikely that they could be solved in polynomial time. We will discuss some of such problems: unlinking and splitting by crossing changes; link equivalence by Reidemeister moves; detecting sublinks with various properties.
We are starting Zoom at 4:45 pm to give those faculty unable to schedule a one-on-one with the speaker time to meet and greet prior to the talk.
Dr. Anastasiia Tsvietkova
Rutgers University, Newark
Intrinsic Geometry, Topology and Complexity of 3-manifolds
Friday, February 19, 2021, 5:00pm
Online
Abstract: Every 3-manifold can be canonically decomposed into pieces, and each piece has a certain geometric structure (Geometrization Theorem). Thus, on a global scale, one can match topological information for the manifold with the respective geometry. However, on a local scale, i.e. intrinsically, the interplay between geometric, topological, and combinatorial properties of a 3-manifold often is not well understood. In this talk, we will focus on one topic in this framework: how the number of surfaces embedded in a 3-manifold is related to the hyperbolic volume and combinatorial "complexity" (number of crossings or number of tetrahedra) of a 3-manifold.
While results of this nature are of interest in low-dimensional geometry and topology, the obtained insight canhelpto establish connections with other areas of mathematics. Among these areas are quantum topology, differential geometry, representation theory, number theory and computational complexity theory. If the time allows, we will briefly discuss some of these connections.
Dr. Ying Wang
University of Oklahoma
An Underground Oil Recovery Model
Monday, February 15, 2021, 5:00pm
Online
Abstract: In this talk, I will discuss an underground oil recovery model whichincludes a third-order mixed derivatives term resulting from the dynamic effects in the pressure difference between the two phases. Analytic study on the computational domain reduction will be provided. A variety of numerical examples will be given. They show that the solutions may have many different saturation profiles depending on the initial conditions, diffusion parameter, and the third-order mixed derivatives parameter. The results are consistent with the study of traveling wave solutions and their bifurcation diagrams.
Ernesto Lupercio
Center for Research and Advanced Studies of the National Polytechnic Institute (Cinvestav-IPN)
An Introductory Mini Course into Quantum Toric Geometry: Lecture II
Joint IMSA & ICMS HSE Event
Friday, August 28, 2020, 9:00am
Online
Abstract: We will introduce the foundations of Quantum Toric Geometry as developed by Katzarkov, Lupercio, Meersseman and Verjovsky, Quantum toric geometry is a generalization of toric geometry where irrational fans correspond to non-commutative spaces called quantum toric varieties. As non-commutative spaces, Quantum toric varieties are to usual toric varieties what the Quantum torus is to the usual torus.
Lecture II
1. LVM theory
2. Quantum GIT
3. Moduli spaces of toric varieties
References: It is useful to be familiar with toric varieties (for example the book of Fulton).
Artan Sheshmani
Harvard University/IMSA
Atiyah Class and Sheaf Counting on Local Calabi-Yau 4 Folds
Joint IMSA & ICMS HSE Event
Friday, August 28, 2020, 8:00am
Online
Abstract: We discuss Donaldson-Thomas (DT) invariants of torsion sheaves with 2 dimensional support on a smooth projective surface in an ambient non-compact Calabi Yau fourfold given by the total space of a rank 2 bundle on the surface. We prove that in certain cases, when the rank 2 bundle is chosen appropriately, the universal truncated Atiyah class of these codimension 2 sheaves reduces to one, defined over the moduli space of such sheaves realized as torsion codimension 1 sheaves in a noncompact divisor (threefold) embedded in the ambient fourfold. Such reduction property of universal Atiyah class enables us to relate our fourfold DT theory to a reduced DT theory of a threefold and subsequently then to the moduli spaces of sheaves on the base surface. We finally make predictions about modularity of such fourfold invariants when the base surface is an elliptic K3.
Tony Yue YU
Laboratoire de Mathématiques d'Orsay
Frobenius Structure Conjecture and Moduli of Calabi-Yau Pairs
Joint IMSA & ICMS HSE Event
Friday, August 28, 2020, 7:00am
Online
Abstract: I will explain the Frobenius structure conjecture of Gross-Hacking-Keel in mirror symmetry, and an application towards the moduli space of Calabi-Yau pairs. I will show that the naive counts of rational curves in an affine log Calabi-Yau variety U, containing an open algebraic torus, determine in a simple way, a mirror family of log Calabi-Yau varieties, as the spectrum of a commutative associative algebra equipped with a multilinear form.
The structure constants of the algebra are constructed via counting non-archimedean analytic disks in the analytification of U. Furthermore, I will introduce a generalization of the Gelfand-Kapranov-Zelevinsky secondary fan, and show that the mirror family admits a natural compactification and extension over the toric variety associated to the secondary fan, which generalizes the families previously studied by Kapranov-Sturmfels-Zelevinsky and Alexeev in the toric case.
We conjecture that this gives rise to a (nearly uni) versal family of polarized Calabi-Yau pairs (embedded in the moduli space of KSBA stable pairs), and has a surprising consequence that such moduli space is unirational. We prove the stability in dimension two. This is based on arXiv:1908.09861 joint with S. Keel, and arXiv:2008.02299 joint with Hacking and Keel.
Ernesto Lupercio
Center for Research and Advanced Studies of the National Polytechnic Institute (Cinvestav-IPN)
An Introductory Mini Course into Quantum Toric Geometry: Lecture I
Joint IMSA & ICMS HSE Event
Thursday, August 27, 2020, 9:00am
Online
Abstract: We will introduce the foundations of Quantum Toric Geometry as developed by Katzarkov, Lupercio, Meersseman and Verjovsky, Quantum toric geometry is a generalization of toric geometry where irrational fans correspond to non-commutative spaces called quantum toric varieties. As non-commutative spaces, Quantum toric varieties are to usual toric varieties what the Quantum torus is to the usual torus.
Lecture I
1. Introduction
2. Stacks and non-commutative spaces
3. The quantum torus
4. Quantum toric varieties
References: It is useful to be familiar with toric varieties (for example the book of Fulton).
Artan Sheshmani
Harvard University/IMSA
Stable Higher Rank Flag Sheaves on Surfaces
Joint IMSA & ICMS HSE Event
Thursday, August 27, 2020, 8:00am
Online
Abstract: We study moduli space of holomorphic triples f: E_{1}–>E_{2}, composed of (possibly rank > 1) torsion-free sheaves (E_{1}, E_{2}) and a holomorphic map between them, over a smooth complex projective surface S. The triples are equipped with Schmitt stability condition. We prove that when Schmitt stability parameter becomes sufficiently large, the moduli space of triples benefits from having a perfect relative and absolute obstruction theory in some cases (depending on rank of holomorphic torsion-free sheaf E_{1}).
We further generalize our construction to higher-length flags of higher rank sheaves by gluing triple moduli spaces, and extend the earlier work, with Gholampur and Yau, where the obstruction theory of nested Hilbert schemes over the surface was studied. Here we extend the earlier results to the moduli space of flags E_{1}––>E_{2}—>...––>E_{n}, where the maps are injective (by stability). There is a connection, by wallcrossing, between the theory of such higher rank flags, and the theory of Higgs pairs on the surface, which provides the means to relate the flag invariants to the local DT invariants of threefold given by a line bundle over the surface, X :=Tot(L –> S).
Tony Yue YU
Laboratoire de Mathématiques d'Orsay
Frobenius Structure Conjecture and Moduli of Calabi-Yau Pairs
Joint IMSA & ICMS HSE Event
Thursday, August 27, 2020, 7:00am
Online
Abstract: I will explain the Frobenius structure conjecture of Gross-Hacking-Keel in mirror symmetry, and an application towards the moduli space of Calabi-Yau pairs. I will show that the naive counts of rational curves in an affine log Calabi-Yau variety U, containing an open algebraic torus, determine in a simple way, a mirror family of log Calabi-Yau varieties, as the spectrum of a commutative associative algebra equipped with a multilinear form.
The structure constants of the algebra are constructed via counting non-archimedean analytic disks in the analytification of U. Furthermore, I will introduce a generalization of the Gelfand-Kapranov-Zelevinsky secondary fan, and show that the mirror family admits a natural compactification and extension over the toric variety associated to the secondary fan, which generalizes the families previously studied by Kapranov-Sturmfels-Zelevinsky and Alexeev in the toric case.
We conjecture that this gives rise to a (nearly uni) versal family of polarized Calabi-Yau pairs (embedded in the moduli space of KSBA stable pairs), and has a surprising consequence that such moduli space is unirational. We prove the stability in dimension two. This is based on arXiv:1908.09861 joint with S. Keel, and arXiv:2008.02299 joint with Hacking and Keel.
Dr. Tomasz Mrowka
Massachusetts Institute of Technology
Efficiently Representing Homology Classes in Four Dimensional Manifolds
Friday, February 28, 2020, 5:00pm
Ungar Room 402
Abstract: In a simply connected four-dimensional smooth manifold, every two-dimensional homology class is represented by a smooth map from the 2-sphere into the four-manifold. Though the map can be perturbed to be a smooth immersion, it is often impossible for the map to be chosen to be a smooth embedding.
Gauge theory and related ideas have provided good estimates for the minimal genus of a 2-dimensional surface which does embed representing a given homology class. The related question of the minimal number of double points of a smooth immersion is less studied. I will try to explain why this question might be interesting outside topology and mention some ongoing work with Peter Kronheimer and others that might give a tool to address some of these questions.
Dr. Carly Klivans
Brown University
Flow-firing Processes
Monday, February 17, 2020, 5:00pm
Ungar Room 402
Abstract: I will discuss a discrete non-deterministic flow-firing process for topological cell complexes. The process is a form of discrete diffusion; a flow is repeatedly diverted according to a discrete Laplacian. The process is also an instance of higher-dimensional chip-firing. I will motivate and introduce the system and then focus on two important features – whether or not the system is terminating and whether or not the system is confluent. We will see how the topology of the space influences these properties.
Dr. Mina Teicher
Dr. Gabriela Olmedo
University of Miami
Mathematics & Biomedicine
IMSA Special Evening
Thursday, January 30, 2020, 5:30pm
Newman Alumni Center, First Floor
Abstract: Dr. Mina Teicher's Abstract: Mathematics is everywhere! In manmade systems and in God made systems. In this talk Dr. Teicher will demonstrate appearance of mathematical forms and logic in nature (humans, plants, stones,...). Moreover, she will describe practical application of math to medicine and to the understanding of the human brain.
Dr. Gabriela Olmedo's Abstract: Why would researchers from biology, physics and mathematics join to study invisible microorganisms? Bacteria organize typically in complex communities that are not only essential for all the biogeochemical cycles on Earth and our health. They also hold clues to the story of life. Two crucial questions in biology are: How can thousands of species coexist in communities and what the rules are for their organization.
Dr. Ruimeng Hu
Columbia University
Deep Fictitious Play for Stochastic Differential Games
Monday, December 9, 2019, 5:00pm
Ungar Room 402
Abstract: Differential games, as an offspring of game theory and optimal control, provide the modeling and analysis of conflict in the context of a dynamical system. Computing Nash equilibria is one of the core objectives in differential games, with a major bottleneck coming from the notorious intractability of N-player games, also known by the curse of dimensionality. To overcome this difficulty, we apply the idea of fictitious play to design deep neural networks (DNNs), and develop deep learning theory and algorithms, for which we refer as deep fictitious play. The resulted deep learning algorithm is scalable, parallelizable and model-free. We illustrate the performance of proposed algorithms by comparing them to the closed-form solution of the linear-quadratic game. We also prove the convergence of the fictitious play under appropriate assumptions and verify that the convergent limit forms an open-loop Nash equilibrium. Based on the formulation by backward stochastic differential equations, we extend the strategy of deep fictitious play to compute closed-loop Markovian Nash equilibrium for both homogeneous and heterogeneous large N-player games.
Dr. Bahman Angoshtari
University of Washington
Two Stochastic Control Problems Motivated by Institutional Investment Management
Friday, December 6, 2019, 5:00pm
Ungar Room 402
Abstract: In this talk, I present two applications of stochastic optimal control theory in investment. The first is a model for optimally trading futures contracts, which are a popular class of financial assets among active investors such as hedge funds. The novelty of the model is in the way the futures prices are modeled by stopped Brownian bridge processes. The optimal trading strategies are subsequently determined from a stochastic control problem, and through analyzing the associated Hamilton-Jacobi-Bellman partial differential equation. The optimal strategy takes a short (resp. long) position in a futures contract if it is in contango (resp. backwardation), which is consistent with the trading rules followed by finance practitioners.
In the second part of the talk, I consider a problem faced by a company's management team in deciding how to distribute dividends. In contrast to previous optimal dividend models, it is additionally assumed that shareholders will not accept dividend rates that fall below a fixed proportion of the maximum dividend rate they have received in the past, resulting in a so-called "drawdown" constraint. I will then formulate a stochastic control problem, reduce it to a nonlinear free-boundary problem, and obtain a semi-explicit solution via the Legendre transform. The optimal policy has an intuitive structure in that it is mainly driven by the ratio of the company's surplus over the maximum past dividend rate. In particular, there are critical values of this ratio that determine when it is optimal to distribute dividend at the minimum acceptable rate, when the dividend rate should be above the minimum, and when it is optimal to raise the dividend rate above its historical maximum.
The talk is based on joint works with Erhan Bayraktar, Tim Leung, and Virginia Young.
Dr. Oleksii Mostovyi
University of Connecticut
Utility Maximization in Incomplete Markets
Wednesday, December 4, 2019, 5:00pm
Ungar Room 402
Abstract: We will start with an introduction to the expected utility maximization problem and a discussion of several approaches for its analysis. Then we will present the standard conclusions of the utility maximization theory followed by the necessary and sufficient conditions for the validity of such conclusions. In the remaining part of the talk, we will discuss the stability and asymptotic analysis of the utility maximization problem. For the perturbations with respect to the market price of risk, we provide a second-order expansion of the value function, a first-order approximation of the terminal wealth, and construct trading strategies that match the indirect utility function up to the second order. We augment these results by examples and a discussion of further characterizations, extensions, and applications.
Alexander Volberg
University of California, Berkeley
Discrete and Continuous Ranking Models
Monday, December 2, 2019, 5:00pm
Ungar Room 402
Abstract: In this talk, I will discuss two different "ranking" models: Mallows' ranking model and rank-dependent diffusions. In the first part, I will discuss the rank-dependent diffusions. I will focus on two models: Up the River model, and N-player games with fuel constraints. These problems require treating carefully the corresponding PDEs. The former is joint with Li-Cheng Tsai, and the latter joint with Xin Guo and Renyuan Xu.
In the second part, I will focus on the Mallows' permutation, and various generalizations. In particular, I will talk about a general model, called regenerative permutations. I will also discuss the statistical properties and algorithms of these Mallows' type ranking models. This is partly joint with Jim Pitman.
If time permits, I will discuss recent progress on the random walk derived from random permutations, which is motivated by applications in systems biology.
Alexander Volberg
Michigan State University
Harmonic Measures and Harmonic Analysis
Thursday, November 21, 2019, 5:00pm
Ungar Room 402
Abstract: Paraproducts are arguably the simplest singular operators. But the standard Calderon-Zygmund theory fails to apply in the product setting. On the other hand, in PDE the need for such multi-parameter singular integral operators appears very naturally when one needs a Leibniz rule for non-homogeneous derivatives, say on product of two functions each of two variables. Obviously it is an absolutely fundamental question. Another need for multi-parameter weighted paraproducts appear from complex analysis in polydisc as in Chang-Fefferman series of papers on Hardy spaces on the polydisc. While embedding Dirichlet space on polydisc into L 2 on torus with respect to a given measure, we stumble upon a counterintuitive property of planar measures that seems to be contradictory to Carleson quilts example in Chang-Fefferman theory. Of course it is not, and our property gives necessary and sufficient condition for boundedness of weighted bi-parameter paraproducts, thus solving the problem of embedding of Dirichlet space of analytic functions on bidisc.
Philippe G. LeFloch
Sorbonne University, France
A Geometric Analysis View on Spacetimes: Stability and Singularities
Thursday, November 14, 2019, 5:00pm
Ungar Room 402
Abstract: I will overview recent mathematical advances on the Einstein equations of general relativity, especially for solutions with low decay or low regularity. We will offer some answers to the following questions.
Are self-gravitating matter fields nonlinearly stable near Minkowski spacetime? What happens when two gravitational waves collide? Can we extend a spacetime beyond a singularity hypersurface?
Blog: http://philippelefloch.org
Mohammed Abouzaid
Colombia University
From Numbers to Spaces in Floer Theory
IMSA Colloquium
Thursday, September 5, 2019, 5:00pm
Ungar Room 528B
Abstract: I will describe the development of Floer theory over the last 30 years as a progression of refined invariants starting with numbers, and rising to categories stably enriched in spaces. At each step, I will introduce some geometric question whose answer is made possible by the additional structure at hand.
Arnaud Ducrot
Univerity of Le Havre, France
Some Results on an Evolutionary-epidemic Problem Arising in Plant Disease
Thursday, May 16, 2019, 5:00pm
Ungar Room 402
Abstract: In this talk we discuss various properties of an evolutionary-epidemic system modelling plant disease epidemic and incorporating the ability of the pathogen to adapt to the environment by mutation. The resulting problem consists in an intregro-differential system of equations that typically depends on a small parameter $\varepsilon>0$ that describes the dispersion of the pathogen in the phenotype trait space.
In the first part of this talk, we show that the system asymptotically stabilizes toward its unique endemic equilibrium and we describe, using a small parameter ($\varepsilon$) asymptotic, a possibly long transient behaviour before reaching the endemic equilibrium.
In the second part, the above problem is extended to the case where the populations are also structured with respect to physical space and where the infection is able to disperse. In that setting, we discuss the spatio-temporal evolution of the disease by studying some properties of the travelling wave solutions for this system, that models the spatial spread of the disease.
Pierre Magal
Univerity of Bordeaux, France
Existence of Wave Trains for the Gurtin-McCamy Equation
Tuesday, May 14, 2019, 5:00pm
Ungar Room 402
Abstract: This work is mainly motivated by the study of periodic wave train solutions for the so-called Gurtin-McCamy equation. To that aim we construct a smooth center manifold for a rather general class of abstract second order semi-linear differential equations involving non-densely defined operators. We revisit results on commutative sums of linear operators using the integrated semigroup theory. These results are used to reformulate the notion of the weak solutions of the problem. We also derive a suitable fixed point formulation for the graph of the local center manifold that allows us to conclude to the existence and smoothness of such a local invariant manifold. Then we derive a Hopf bifurcation theorem for second order semi-linear equations. This result is applied to study the existence of periodic wave trains for the Gurtin-McCamy problem, that is for a class of non-local age structured equations with diffusion.
Dr. Alex Iosevich
Univerity of Rochester
Analytic and Combinatotorial Aspects of Finite Point Configurations
Thursday, April 18, 2019, 5:00pm
Ungar Room 402
Abstract: We are going to discuss the following basic question. How large does a subset of a vector space need to be to ensure that it determines a positive proportion of all possible point configurations of a given type, where the notion of large depends on the structure of the underlying field. We shall discuss the analytic and combinatorial aspects of this problem, describe some recent results and applications to problems in classical analysis involving the existence and non-existence of exponential bases and frames.
Dr. Andrew Morozov
Univerity of Leicester
Towards Constructing a Mathematically Rigorous Framework for Modeling Evolutionary Fitness
Thursday, April 11, 2019, 5:00pm
Ungar Room 402
Abstract: In modelling biological evolution, a major mathematical challenge consists in an adequate quantification of selective advantages of species. Current approaches to modelling natural section are often based on the idea of maximization of a certain prescribed criterion – evolutionary fitness. This paradigm was inspired by the seminal Darwin's idea of the 'survival of the fittest'. However, the concept of evolutionary fitness is still somewhat vague, intuitive and is often subjective. On the other hand, by using different definitions of fitness one can predict conflicting evolutionary outcomes, which is obviously unfortunate. In this talk, I present a novel axiomatic approach to model natural selection in dynamical systems with inheritance in an arbitrary function space. For a generic self-replication system, I introduce a ranking order of inherited units following the underlying measure density dynamics. Using such ranking, it becomes possible to derive a generalized fitness function which maximization will predict long-term evolutionary outcome. The approach justifies the variational principle of determining evolutionarily stable behavioural strategies. I demonstrate a new technique allowing to derive evolutionary fitness for population models with structuring (e.g. in models with time delay) which was so far a mathematical challenge. Finally, I show how the method can be applied to a von Foerster continuous stage population model.
CANCELLED
Alexander Volberg
Michigan State Univerity
Poincare Inequalities on Hamming Cube and Related Combinatorial and Probabilistic Problems
Thursday, March 28, 2019, 5:00pm
Ungar Room 402
Abstract: Geometric inequalities on Hamming cube imply corresponding isoperimetric inequalities in Gaussian spaces. Inequalities in discrete setting (on Hamming cube) are usually more difficult and more deep. In particular, Poincaré inequalities on Hamming cube give sharp lower estimates for the product measure of the boundaries of arbitrary sets of Hamming cube. Such estimates were used by Margulis in his famous network connectivity theorem. We will survey such estimates obtained by Margulis, Bobkov, Ledoux, Lust-Piquard. Recently the constant in L 1 discrete Poincaré inequality was improved. The sharp constant remains unknown (unlike the Gaussian case, where it was found by Maurey–Pisier and then Ledoux), but we will show the idea of the improvement.
Professor Fedor Bogomolov
New York Univerity
On Projective Invariants of k-tuples of Torsion Points on Elliptic Curves
Tuesday, March 19, 2019, 5:00pm
Ungar Room 402
Abstract: Every complex elliptic curve $E$ has a natural (so called hyperlliptic) involution $\theta$ (as an abelian group and algebraic curve) with $4$ stable points and $P^1$ as quotient $E/\theta$. The stable points of $\theta$ can be identified with a subgroup of points of order $2$ on $E$ with a torsion subgroup $Q/Z+ Q/Z\subset E$.
The problem which I am going to consider is about the variation of the images of collections of points from $Q/Z+ Q/Z$ in $P^1$ which occur under the variation of elliptic curve $E_t$.
We are conidering more precisely the variation of projective invariants of such collections. Thus the problem becomes interesting when the number of corresponding points in $P^1$ is $\geq 4$.
In our joint work with Yuri Tschinkel and Hang Fu we formulated several conjecture conecerning the behavior of such sets.
In our recent article with Hang Fu we managed to describe all collections of $4$-tuples for which the variation of projective invariants is trivial.
I will discuss the proof and description of such $4$-tuples in my talk and several other general concepts and results related to the subject.
Sergey Fomin
Univerity of Michigan
Morsifications and Mutations
Friday, March 1, 2019, 5:00pm
Ungar Room 402
Abstract: I will discuss a new and somewhat mysterious connection between singularity theory and cluster algebras, more specifically between the topology of isolated singularities of plane curves and the mutation equivalence of quivers associated with their morsifications. This is joint work with Pavlo Pylyavskyy, Eugenii Shustin, and Dylan Thurston.
David Zureick-Brown
Emory Univerity
Diophantine and tropical Geometry
Thursday, February, 21, 2019, 5:00pm
Ungar Room 402
Abstract: Diophantine geometry is the study of integral solutions to a polynomial equation. For instance, for integers a,b,c ≥ 2 satisfying 1/a + 1/b + 1/c > 1, Darmon and Granville proved that the individual generalized Fermat equation x^a + y^b = z^c has only finitely many coprime integer solutions. Conjecturally something stronger is true: for a,b,c ≥ 3 there are no non-trivial solutions.
I'll discuss various other Diophantine problems, with a focus on the underlying intuition and conjectural framework. I will especially focus on the uniformity conjecture, and will explain new ideas from tropical geometry and our recent partial proof of the uniformity conjecture.
David Eisenbud
University of California, Berkeley
Residual Intersections, Old and New
Friday, February, 15, 2019, 5:00pm
Ungar Room 402
Abstract: Two general quadric hypersurface in complex 3-space that contain a line, intersect in the line and also a curve of degree 3, the "residual intersection". I'll describe the 19th-century motivations and origins of the theory of residual intersections, and also some recent work in the area.
Dr. Akram S. Alishahi
Ritt Assistant Professor at Columbia University
Homological Know Invariants, Relations and Applications
Wednesday, December 12, 2018, 3:00pm
Ungar Room 402
Abstract: Knot theory is about studying knots i.e. image of a smooth injective map from circle to R^3. In this talk, we will start by sketching some problems in knot theory. Then we will discuss two knot invariants, Khovanov homology and knot Floer homology, and we will explain how they can be used to answer some of these questions.
Khovanov homology and knot Floer homology are algebraic knot invariants that are defined combinatorially and analytically, respectively. Despite their very different definitions, the two invariants seem to contain a great deal of the same information and are conjectured to be related. In parallel, we will discuss some of their similarities. This talk is based on joint works with Nathan Dowlin and Eaman Eftekhary.
Dr. Jeffrey Meier
Postdoctoral Associate
University of Georgia
Generalized Square Knots and Homotopy 4-spheres
Monday, December 10, 2018, 5:00pm
Ungar Room 402
Abstract: Perhaps the most elusive open problem in low-dimensional topology is the smooth 4-dimensional Poincare Conjecture, which asserts that any 4-manifold with the homotopy type of the 4-sphere is diffeomorphic to the 4-sphere. For the last forty years, potential counterexamples to this conjecture have been constructed, illustrated, and subsequently standardized. Many of these examples are geometrically simply connected, meaning they can be built without 1-handles. If such a homotopy 4-sphere is built with only one 2-handle, then it must be the 4-sphere; this is a consequence of David Gabai's solution to the Property R Conjecture.
In this talk, I will discuss work to understand geometrically simply connected homotopy 4-spheres that are built with two 2-handles. In the case that one of the 2-handles is attached along a fibered knot, we obtain strong results about the nature of the second component. Building on this, we use the beautiful periodic structure of torus knots to classify the attaching curve of the second component when the first component is a generalized square knot (a torus knot summed with its mirror). Finally, we prove that for an infinite family of such links, the corresponding homotopy 4-sphere is the standard one, proving the Poincare Conjecture in this setting. We also give intriguing new potential counterexamples to the Poincare Conjecture coming from these families. This talk is based on joint work with Alex Zupan.
Dr. Libin Rong
University of Florida
Modeling HIV Dynamics under Treatment
Thursday, December 6, 2018, 5:00pm
Ungar Room 402
Abstract: Highly active antiretroviral therapy has successfully controlled HIV replication in many patients. The treatment effectiveness depends on many factors, such as pharmacokinetics/pharmacodynamics of drugs and the intracellular stages of the viral replication cycle inhibited by antiretroviral drugs. In this talk, I will present some recent work on studying HIV dynamics under treatment. Using multi-stage models, I will show that drugs from different classes have different influence on HIV decay dynamics. Using models that combine pharmacodynamics and virus dynamics, I will show that pharmacodynamic profiles of drugs can significantly affect the outcome of either early or late treatment of HIV infection.
Dr. Marco A. M. Guaraco
L. E. Dickson Instructor at the University of Chicago
Member of the Institute for Advanced Study
Phase Transitions and Minimal Hypersurfaces
Monday, December 3, 2018, 5:00pm
Ungar Room 402
Abstract: Long standing questions in the theory of minimal hypersurfaces have been solved in the past few years. This progress can be explained and enriched through a strong analogy with the theory of phase transitions. I will present the current state of these ideas, discuss my contributions to the subject and share directions for future developments.
Dr. Christopher Scaduto
Joint Assistant Professor and NSF Postdoctoral Fellow
Simons Center for Geometry and Physics at Stony Brook University
Instantons and Lattices of Smooth 4-manifolds with Boundary
Thursday, November 29th, 2018, 5:00pm
Ungar Room 402
Abstract: A classical invariant associated to a 4-manifold is the intersection form on its second homology group, which is an integral lattice. A famous result of Donaldson from the early 1980s says that a definite lattice of a smooth compact 4-manifold without boundary is diagonalizable over the integers. What if there is non-empty boundary? This talk surveys recent advances on this problem which have been obtained using Yang-Mills instanton Floer theory.
Dr. Siyuan Lu
Rutgers University
Isometric Embedding and Quasi-local Mass
Tuesday, November 27, 2018, 5:00pm
Ungar Room 402
Abstract: In this talk, we will first review the classic result of isometric embedding of (S^2,g) into 3-dimensional Euclidean space by Nirenberg and Pogorelov. We will then discuss how to apply it to define quasi-local mass in general relativity. In particular, the positivity of Brown-York quasi-local mass proved by Shi-Tam is equivalent to the Riemannian Positive mass theorem by Schoen-Yau and Witten.
We will then discuss the recent progress in isometric embedding of (S^2,g) into general Riemannian manifold. We will also discuss the recent work on a localized Riemannian Penrose inequality, which is equivalent to the Riemannian Penrose inequality.
CANCELLED
David Zureick-Brown
Emory University
Diophantine and Topical Geometry
Thursday, November 8, 2018, 5:00pm
Ungar Room 402
Abstract: Diophantine geometry is the study of integral solutions to a polynomial equation. For instance, for integers a,b,c ≥ 2 satisfying 1/a + 1/b + 1/c > 1, Darmon and Granville proved that the individual generalized Fermat equation x^a + y^b = z^c has only finitely many coprime integer solutions. Conjecturally something stronger is true: for a,b,c ≥ 3 there are no non-trivial solutions. I'll discuss various other Diophantine problems, with a focus on the underlying intuition and conjectural framework. I will especially focus on the uniformity conjecture, and will explain new ideas from tropical geometry and our recent partial proof of the uniformity conjecture.
David Herzog
Iowa State University
Ergodicity and Lyapunov Functions for Langevin Dynamics with Singular Potentials
Thursday, September 27, 2018, 5:00pm
Ungar Room 402
Abstract: We discuss Langevin dynamics of N particles on R^d interacting through a singular repulsive potential, e.g. the well-known Lennard-Jones type, and show that the system converges to the unique invariant Gibbs measure exponentially fast in a weighted total variation distance. The proof of the result turns on an explicit construction of a Lyapunov function. In contrast to previous results for such systems, our result implies geometric convergence to equilibrium starting from an essentially optimal family of initial distributions.
Dr. Damian Brotbek
University of Strasbourg
Hyperbolicity and Jet Differentials
Tuesday, June 5, 2018, 2:30pm
Ungar Room 402
Abstract: In the 60's, Kobayashi introduced on any complex manifold X an intrinsic pseudo-metric generalizing the Poincaré metric on the unit disc. When this pseudo metric is in fact a metric, the manifold X is said to be hyperbolic in the sense of Kobayashi. By a result of Brody, when X is compact, then it is hyperbolic if and only if it does not contain any entire curve (a non constant holomorphic map from the complex plane to X).
A fruitful way to study hyperbolicity problems is to use jet differential equations. Those objects, generalizing symmetric differential forms, provide obstructions to the existence of entire curves and can be used in some particular situation to prove that some given varieties is hyperbolic.
The purpose of this talk, aimed at a general audience, is to give an overview on hyperbolicity and the theory of jet differentials.
Michael Larsen
Indiana University
The Circle Method in Algebraic Geometry
Monday, May 7, 2018, 5:00pm
Ungar Room 402
Abstract: Certain counting problems in group theory can be formulated either in terms of varieties over finite fields, or (dually) in terms of irreducible character values. By comparing the two points of view, one can either use geometry to give character estimates or (what I will mostly talk about) character estimates to prove theorems in geometry.
Ayelet Lindenstrauss
Indiana University
Cohomology Theories and Topological Hochschild Homology
Monday, May 7, 2018, 3:30pm
Ungar Room 402
Abstract: Cohomology theories assign to every space a graded abelian group, satisfying appropriate axioms. Particularly nice ones have a product, that is: they assign to every space a graded ring. It turns out that such theories can be described in terms of ring spectra. Modern constructions let us define actual products that are both associative and unital on the ring spectra that correspond to multiplicative cohomology theories, which is harder than one would think due to some "flabbiness" in the definition of the ring spectra. Using these products, though, we can look at the ring spectra of discrete rings (corresponding to the usual cohomology of a space with coefficients in that ring) and replicate homological algebra constructions on the discrete rings with topological constructions on the corresponding ring spectra. The integers are an initial object in the category of discrete unital rings; in the category of ring spectra, that role is played by the sphere spectrum. So even if we are only interested in understanding discrete rings, doing homological algebra with their ring spectra over the sphere spectrum turns out to give new and interesting constructions.
Topological Hochschild homology is the ring spectrum version of Hochschild homology, with tensor products taken over the sphere spectrum rather than over the integers. It is a finer invariant of discrete rings, and the Dennis trace map from algebraic K-theory to Hochschild homology can be applied to ring spectra and thus factors through Topological Hochschild homology. I will discuss the topological Hochschild homology of rings including number rings (joint with Ib Madsen) and maximal orders in simple algebras over the rationals (joint with Henry Chan).
Professor Takayuki Hibi
Osaka University
Reflexive Polytopes
Monday, April 30, 2018, 5:00pm
Ungar Room 402
Abstract: A lattice polytope P of dimension d in the d-dimensional euclidean space is called reflexive if the origin is contained in the interior of P and if the dual polytope of P is again a lattice polytope. For example, the triangle in the euclidean plane with the vertices (-1,-1), (-1,2) and (2,-1) is reflexive. It turns out that reflexive polytopes play an important role in various areas of mathematics. One of the questions in combinatorics is how to construct reflexive polytopes in natural ways. In my talk, in the frame of Gröbner bases, a technique to yield reflexive polytopes will be discussed. No special knowledge will be required to understand my talk.
James McKernan
University of California, San Diego
Symmetries of Polynomials
Thursday, April 26, 2018, 5:00pm
Ungar Room 402
Abstract: Symmetries of polynomials are closely connected to the geometry of the variety of zeroes of the polynomials. Varieties come in three types and all three types have very different symmetry groups. We review some results, both old and new, which place bounds on the size of the symmetry group.
Dr. Boris Botvinnik
University of Oregon
Conformal Geometry and Topology of Manifolds
Thursday, April 19, 2018, 5:00pm
Ungar Room 402
Abstract: I will start with basics on conformal geometry, we will discuss the Einstein-Hilbert functional and Yamabe problem. Then I plan to discuss the problem of existence of metrics with positive scalar curvature for simply connected spin manifolds. At the end I would like to describe some recent results on the space of metrics with positive scalar curvature.
Mary Ann Horn
Professor and Chair, Department of Mathematics
Applied Mathematics and Statistics
Case Western Reserve University
Using Mathematical Modeling to Understand the Role of Diacylglycerol (DAG) as a Second Messenger
Thursday, April 12, 2018, 5:00pm
Ungar Room 402
Abstract: Diacylgylcerol (DAG) plays a key role in cellular signaling as a second messenger. In particular, it regulates a variety of cellular processes and the breakdown of the signaling pathway that involves DAG contributes to the development of a variety of diseases, including cancer. A mathematical model of the G-protein signaling pathway in RAW 264.7 macrophages downstream of P2Y6 activation by the ubiquitous signaling nucleotide uridine 5'-diphosphate is presented. The primary goal is to better understand the role of diacylglycerol in the signaling pathway and the underlying biological dynamics that cannot always be easily measured experimentally. The model is based on time-course measurements of P2Y6 surface receptors, inositol trisphosphate, cytosolic calcium, and with a particular focus on differential dynamics of multiple species of diacylglycerol. When using the canonical representation, the model predicted that key interactions were missing from the current pathway structure. Indeed, the model suggested that to accurately depict experimental observations, an additional branch to the signaling pathway was needed, whereby an intracellular pool of diacylglycerol is immediately phosphorylated upon stimulation of an extracellular receptor for uridine 5'-diphosphate and subsequently used to aid replenishment of phosphatidylinositol. As a result of sensitivity analysis of the model parameters, key predictions can be made regarding which of these parameters are the most sensitive to perturbations and are therefore most responsible for output uncertainty. (Joint work with Hannah Callender, University of Portland, and the H. Alex Brown Lab, Vanderbilt.)
Iosif Polterovich
Professor, Universite de Montreal
Canada Research Chair in Geometry and Spectral Theory
Sloshing, Steklov, and Corners
Thursday, April 5, 2018, 5:00pm
Ungar Room 402
Abstract: The sloshing problem is a Steklov type eigenvalue problem describing small oscillations of an ideal fluid. We will give an overview of some latest advances in the study of Steklov and sloshing spectral asymptotics, highlighting the effects arising from corners, which appear naturally in the context of sloshing. In particular, we will discuss the proofs of the conjectures posed by Fox and Kuttler back in 1983 on the asymptotics of sloshing frequencies in two dimensions. We will also outline an approach towards obtaining sharp asymptotics for Steklov eigenvalues on polygons. The talk is based on a joint work with M. Levitin, L. Parnovski and D. Sher.
Professor Fu Liu
University of California, Davis
Ehrhart Positivity
Tuesday, April 3, 2018, 5:00pm
Ungar Room 402
Abstract: The Ehrhart polynomial counts the number of lattice points inside dilation of an integral polytope, that is, a polytope whose vertices are lattice points. We say a polytope is Ehrhart positive if its Ehrhart polynomial has positive coefficients. In the literature, different families of polytopes have been shown to be Ehrhart positive using different techniques. We will survey these results in the first part of the talk, after giving a brief introduction to polytopes and Ehrhart polynomials.
Through work of Danilov/McMullen, there is an interpretation of Ehrhart coefficients relating to the normalized volumes of faces. In the second part of the talk, I will discuss joint work with Castillo in which we try to make this relation more explicit in the case of regular permutohedra. The motivation is to prove Ehrhart positivity for generalized permutohedra. If time permits, I will also discuss some other related questions.
Robert Bryant
Phillip Griffiths Professor of Mathematics
Duke University
On Self-Dual Curves
Friday, March 2, 2018, 5:00pm
Fieldhouse at the Watsco Center
Abstract: An algebraic curve in the projective plane (or, more generally in a higher dimensional projective space) is said to be 'self-dual' if it is projectively equivalent to its dual curve (after, possibly, an automorphism of the curve). Familiar examples are the nonsingular conics (or, more generally, rational normal curves in higher dimensions) and the 'binomial curves' y^a = x^b, but there are many more such curves, even in the plane.
I'll survey some of the literature on these curves, particularly in the plane and 3-space, and some of what is known about their classification and moduli, including their connection with contact curves in certain contact 3-folds, some of which are singular. I'll also provide what appear to be some new examples of these curves.
Michael Li
Applied Math Institute
University of Alberta
Nonidentifiability Issue in Parameter Estimation of Differential Equation Models
Thursday, February 22, 2018, 2:00pm
Ungar Room 402
Abstract: Transmission models for infectious diseases using differential equations are frequently confronted with disease data. For instance, these type of models are used to analyze HIV surveillance data, for the assessment of HIV epidemics and estimation of true burden of HIV in terms of incidence, prevalence and the size of undiagnosed HIV positive population. Parameter estimation when fitting the model to data is a key step of the modelling approach, and can often be complicated by the the presence of nonidentifiable parameters. Nonidentifiability results in multiple, often infinitely many, parameter values for which the model fit the data equally well, while different choices of these best-fit parameter values can produce very different model predictions for unobserved quantities of public health interest.
In this talk, I will begin by discussing various notions of nonidentifiability: structural vs practical,local vs global, etc, and different methods to detect and diagnose nonidentifiability. Then I will present a new mathematical approach to study the issue of nonidentifiability based on singular value decomposition and variance decomposition. I will then illustrate our approach with a case study of HIV estimation using an ordinary differential equation model. Some open questions for infinite dimensional models such as delay differential equation and partial differential equation models will also be discussed.
Dr. Simon Gindikin
Rutgers University
Curved Version of the Radon Inversion Formula
Thursday, February 15, 2018, 5:00pm
Ungar Room 402
Abstract: 100 years ago Radon published his famous formula for the reconstruction of functions on the plane through their integrals along lines. Is it possible, to replace in this construction lines with different curves? There are only known just a few such examples, such as geodesicsor horocycles on the hyperbolic plane. These formulas usually look similar to the Radon's formula. We give a universal reconstruction formula, as a closed differential form on the manifold of all curves, whose restriction on different cycles of curves gives specific examples of inversion formulas for curves. It is possible to interpret this construction as areal Cauchy integral formula.
Professor Yipeng Jing
Academician, The Chinese Academy of Sciences
Shanghai Jiao Tong University
Probing the Cosmic Expansion with Large Scale Galaxy Surveys:
Prospects and Challenges
Tuesday, January 30, 2018, 5:00pm
Ungar Room 402
Abstract: The Universe is found to be expanding in an accelerating phase. Mysterious dark energy is one possible solution to explain the acceleration, and modifying the gravity theory is another. In order to find out what is driving the cosmic accelerating expansion, one has to first answer the question whether the General Relativity is still valid on the cosmic scales. Astronomers are carrying out this test by observing many millions galaxies. I will introduce the basic information of this observation and summarize the current status. I will also introduce the future observations, and finally outline theoretical and observational challenges.
Professor Ziv Ran
University of California, Riverside
Filling Groovy:
The Goodness of Generic Projections
Thursday, December 14, 2017, 5:00pm
Ungar Room 402
Abstract: The classical process of projection amounts to selecting a linear subspace W from a given vector space V of functions on a geometric object X. This is analogous to vision, where W is the 2-dimensional space of coordinate functions on a retina. What information is lost by passing from V to W when W is selected randomly among subspaces of given dimension?
We will describe some progress on a version of this problem in complex algebraic geometry.
Steven Lu
Université du Québec à Montréal
The Structure of Semi-hyperbolic Projective Algebraic Manifolds
Thursday, April 27, 2017, 5:00pm
Ungar Room 402
Abstract: S. Kobayashi coined the term hyperbolic for a compact complex manifold M without nontrivial holomorphic images of C and conjectured the positivity of the canonical bundle of M. In particular M would be projective if true. But the conjecture is still wide open for projective manifolds beyond dimension two.
A spectacular advance in this direction is the resolution in the projective case by D. Wu-S.T. Yau (Invent. 2016) of the differential geometric analog of the conjecture, due to S.T. Yau. The analog pertains to compact Kähler manifolds with negative holomorphic curvature and the said advance resolves in particular the abundance conjecture, a key conjecture for the classification of algebraic varieties, for such a manifold.
In this talk, I will mainly focus on a recent joint paper with G. Heier, B. Wong and F.Y. Zheng that offers a structure theorem for projective Kähler manifolds with negative holomorphic curvature, assuming the abundance conjecture. The analysis involves a careful study of the rank of the said curvature, and offers relationships to the global abundance problem.
Dr. Nancy Rodriguez
University of North Carolina
On the Obstruction and Propagation of Entire Solutions to a Non-local Reaction Diffusion Equation with a Gap
Thursday, April 13, 2017, 5:00pm
Ungar Room 402
Abstract: In this talk I will discuss the propagation properties of a bistable spatially heterogeneous reaction-diffusion equation where the diffusion is generated by a jump process. Here the spatial heterogeneity is due to a small region with decay. First, I will focus on the existence and uniqueness of a "generalized transition front". Then I will give some partial results about propagation and obstruction of the transition front. Throughout the talk I will point out many interesting differences between the non-local and local reaction-diffusion equations.
Pengfei Guan
McGill University
Isometric Embeddings, Geometric Inequalities and Nonlinear PDEs
Wednesday, April 12, 2017, 5:00pm
Ungar Room 402
Abstract: In 1950s, Nirenberg and Pogorelov solved the classical Weyl problem regarding the isometric embedding of positively curved compact surface in to R^3. Solution to Weyl's problem is crucial to the definition of the Brown-York quasi local mass in general relativity in 1990s, and also play key role in the recent works of Liu-Yau and Wang-Yau. The development brings renewed focus on the Weyl problem of isometric embedding of surfaces to general 3D ambient space. We will discuss elliptic PDEs involved the problem and recent work on this type of nonlinear equations. We also discuss new proof of isoperimetric type of inequalities using parabolic PDEs. The talk is try to illustrate some beautiful interaction of nonlinear PDE, differential geometry and general relativity. It is accessible for general mathematical audience.
Dr. Alexander Kiselev
Rice University
Enhancement of Biological Reactions by Chemotaxis
Thursday, April 6, 2017, 5:00pm
Ungar Room 402
Abstract: Many reactions and processes in nature take place in fluid and in presence of both fluid flow and chemotaxis - directed motion of cells or species guided by attractive (or repulsive) chemical. One example of such process is broadcast spawning by corals, the way corals reproduce. Models of this process based on pure reaction-diffusion tend to dramatically underestimate the fertilization success rate. I will discuss a simplified 2D single equation model which incorporates fluid flow and chemotaxis effects. In the framework of this model built on the basis of the well known Keller-Segel equation, the role of chemotaxis turns out to be crucial. In the presence of a sufficiently strong chemotaxis, even weakly coupled reaction can lead to high fertilization rate on a fixed time scale.
If time permits, I will discuss some progress in a more sophisticated model which involves a system of two equations. Novel mathematical tools used in this work involve sharp convergence to equilibrium estimates for a class of Fokker-Planck operators with logarithmic-type potentials.
Anders Björner
KTH Royal Institute of Technology, Sweden
Around Codimension One Embeddings
Tuesday, March 7, 2017, 5:00pm
Ungar Room 402
Abstract: Being drawable in the plane without intersecting edges is a very important and much studied graph property. Euler observed in 1752 that planarity implies a linear upper bound on the number of edges of a graph (which otherwise is quadratic in the number of vertices). Several ways of characterizing planar graphs have been given during the previous century.
Planarity is, of course, a special case of a general notion of embedding a simplicial d-complex into real k-space. The k=d+1 and k=2d cases are of particular interest in higher dimensions, since they both generalize planarity. Embedding a space into some manifold is a much studied question in geometry/topology. For instance, van Kampen showed that in the k=2d case there is a very useful cohomological obstruction to embeddability.
Higher-dimensional embeddability has been studied also from the combinatorial point of view, in a tradition inspired by Euler. In this talk I will survey a few topics from the combinatorial study of embeddings, such as bounds for the number of maximal faces and algorithmic questions. I will end with mention of some joint work with A. Goodarzi concerning an obstruction to k=d+1 embeddings.
The talk will not presuppose previous familiarity with the topic.
Simon A. Levin
Princeton University
Collective Motion, Collective Decision-making, and Collective Action
Friday, March 3, 2017, 4:00pm
Ungar Room 402
Abstract: There exists a rich history of research on the mathematical modeling of animal populations. The classical literature, however, is inadequate to explain observed spatial patterning, or foraging and anti-predator behavior, because animals actively aggregate. This lecture will begin from models of animal aggregation, the role of leadership in collective motion and the evolution of collective behavior, and move from there to implications for decision-making in human societies. Ecological and economic systems are alike in that individual agents compete for limited resources, evolve their behaviors in response to interactions with others, and form exploitative as well as cooperative interactions as a result. In these complex-adaptive systems, macroscopic properties like the flow patterns of resources like nutrients and capital emerge from large numbers of microscopic interactions, and feedback to affect individual behaviors. I will explore common features of these systems, especially as they involve the evolution of cooperation in dealing with public goods, common pool resources and collective movement across systems; Examples and lessons will range from bacteria and slime molds to groups to insurance arrangements in human societies and international agreements on environmental issues.
Ron Adin
Bar Ilan University, Israel
Cyclic Descents, Toric Schur Functions and Gromov-Witten Invariants
Tuesday, February 28, 2017, 5:00pm
Ungar Room 402
Abstract: Descents of permutations have been studied since Euler. This notion has been vastly generalized in several directions, and in particular to the context of standard Young tableaux (SYT). More recently, cyclic descents of permutations were introduced by Cellini and further studied by Dilks, Petersen and Stembridge. Looking for a corresponding notion for SYT, Rhoades found a very elegant solution for rectangular shapes.
In an attempt to extend this concept, explicit combinatorial definitions for two-row and certain other shapes have been found, implying the Schur-positivity of various quasi-symmetric functions. In all cases, the cyclic descent set admits a cyclic group action and restricts to the usual descent set when the letter $n$ is ignored. Consequently, the existence of a cyclic descent set with these properties was conjectured for all shapes, even the skew ones.
This talk will report on the surprising resolution of this conjecture: Cyclic descent sets do exist for nearly all skew shapes, with an interesting small set of exceptions. The proof applies nonnegativity properties of Postnikov's toric Schur polynomials and a new combinatorial interpretation of certain Gromov-Witten invariants. We shall also comment on issues of uniqueness.
Joint with Sergi Elizalde, Vic Reiner and Yuval Roichman.
Enrico Arbarello
Università degli Studi di Roma "La Sapienza"
Hyperplane Sections of K3 Surfaces
Friday, February 3, 2017, 5:00pm
Ungar Room 402
Abstract: K3 surfaces and their hyperplane sections play a central role in algebraic geometry. This is a survey of the work done during the past five years to characterize which smooth curves lie on a K3 surface. Related topics will be discussed. These are joint works with a combination of the following authors: Andrea Bruno, Gavril Farkas, Edoardo Sernesi and Giulia Saccà.
Yuri Tschinkel
New York University
Arithmetic and Geometry of Fano Varieties
Thursday, February 2, 2017, 5:00pm
Ungar Room 402
Abstract: I will discuss recent advances in the theory of Fano varieties over nonclosed fields (joint with B. Hassett, A. Kresch, and A. Pirutka).
Dr. Tye Lidman
North Carolina State University
Left-orderability and Three-manifolds
Thursday, January 26, 2017, 5:00pm
Ungar Room 402
Abstract: A group is called left-orderable if it can be given a left-invariant total order. We will discuss the question of when the fundamental group of a three-manifold Y is left-orderable. Orderability is known to be related to certain topological aspects of Y, such as the surfaces which sit inside it. We will discuss a conjectural relationship between left-orderability and the solutions to a certain nonlinear PDE on Y.
Professor Luc Vinet
Centre de Recherches Mathématiques, Montreal
The Bannai-Ito Algebra in Many Guises
Joint Math-Physics Colloquium
Thursday, January 26, 2017, 4:00pm
Physics Conference Room, 3rd Floor
Abstract: This talk will offer a review of the Bannai-Ito algebra and of its higher rank extension. It will first be explained that it is in a Schur-Weyl duality with the super algebra osp(1,2). Its occurrence as the symmetry algebra of the Dirac-Dunkl equation will be discussed and its relation to orthogonal polynomials will also be presented.
John Morgan
Stony Brook University
Spin Manifolds of Dimensions at Most 4
Wednesday, January 25, 2017, 5:00pm
Ungar Room 402
Abstract: Low dimensional spin manifolds are interesting objects with close connections to quadratic forms. The first part of the talk will provide an overview of these manifolds and their invariants. The second part of the talk will use the understanding of low dimensional spin manifolds to give a detailed description of invariants that for each topological space X detect all 3- and 4-dimensional spin manifolds mapping to X up to spin bordism.
Dr. Pierre Magal
University of Bordeaux, France
Final Size of an Epidemic for a Two Group SIR Model
Thursday, December 15, 2016, 4:00pm
Ungar Room 402
Abstract: In this talk we consider a two-group SIR epidemic model. We study the final size of the epidemic for each sub-population. The qualitative behavior of the infected classes at the earlier stage of the epidemic is described with respect to the basic reproduction number. Numerical simulations are also preformed to illustrate our results.
Dr. Andrea Tellini
École des Hautes Études en Sciences Sociales
Enhancement of Fisher-KPP Propagation through Lines and Strips of Fast Diffusion
Wednesday, December 14, 2016, 5:00pm
Ungar Room 402
Abstract: In this talk I will present some systems of reaction-diffusion equations which take into account the presence of diffusion (and/or reaction) heterogeneities in some regions of the domain. The motivation is the modelling of the invasion of an environment by a species whose individuals can move (and/or reproduce) faster in some regions of the habitat. I will describe the dynamics of such systems and focus on the qualitative properties of the propagation speed, showing in particular when it is larger than in the case of a homogeneous environment. These are joint works with H. Berestycki, L. Rossi and E. Valdinoci.
Dr. Xi Huo
York University
Zika Outbreaks in a Highly Heterogeneous Environment: Insights from Dynamical Modelling
Monday, December 12, 2016, 5:00pm
Ungar Room 402
Abstract: Zika virus is in the family of Flaviviridae , and is often transmitted to human by Aedes aegypti, a common vector for transmitting several tropical fevers, including dengue and chikungunya. The environmental heterogeneity and intervention strategies of Zika spread also involve seasonality, co-circulation of other vector-borne diseases, and demographic structures of the mosquito population. We have been developing a variety of dynamical models to understand the transmission dynamics with focus on different aspects of environmental heterogeneities. We first consider the co-infection and co-circulation of dengue and Zika and their implication of dengue vaccination program for Zika control in the presence of experimentally reported antibody-dependent enhancement. We then consider the impact of heterogeneity of vector demographics on the initial outbreak rate and outbreak potential using age-structured partial differential equation systems and calculating the relevant threshold using non-linear semigroup theory and spectral theory. We also examine both numerically and analytically the mechanisms for potential nonlinear oscillations using the global bifurcation theory in delay differential equations.
Dr. William Christopher Strickland
University of North Carolina, Chapel Hill
Modeling Invasive Dispersal at Multiple Scales
Thursday, December 8, 5:00pm
Ungar Room 402
Abstract: Biological invasions represent an interesting challenge to model mathematically. Landscape heterogeneity, non-local and temporally dependent spreading mechanisms, coarse data, and the presence of long-distance transportation connections are but a few of the complications that can greatly affect our understanding of invasive spread. In this talk, I will look at dispersal from a multi-scale perspective in an attempt to address some of these challenges.
To begin, I will introduce a generalization of Mollison’s stochastic contact birth process (J R Stat Soc 39(3):283, 1977) which is robust to non-local distribution kernels and heterogeneity in the landscape. By interpreting the quantity of interest as species occurrence probability rather than population size, I will describe how this process may also be approximated and simulated deterministically, using niche modeling tools to characterize landscape heterogeneity. Adding to this is a method for considering the effects of a disease-vector transportation network, which can unwittingly transport a biological invader to distant sites. Finally, I will shift focus to the intial stages of an invasion and concentrate on the local and mesoscale by considering the intentional release of a parasitoid wasp biocontrol agent. Results indicate that the fluid physics of air above the landscape likely plays a critical role in the dispersal process.
Numerical results will be included throughout the talk, including simulations for the cheatgrass (bromus tectorum) invasion in Rocky Mountain National Park and the initial spread of parasitoid wasps (Eretmocerus hayati) during a biocontrol introduction.
Dr. Jan Sbierski
University of Cambridge
Strong Cosmic Censorship and the Wave Equation in the Interior of Black Holes
Wednesday, December 7, 2016, 5:00pm
Ungar Room 402
Abstract: The Einstein equations admit a locally well-posed initial value problem. However, there are explicit black hole solutions of the Einstein equations for which global uniqueness fails. The strong cosmic censorship conjecture in general relativity states that global uniqueness should hold generically -- which implies the expectation that small perturbations of the initial data for the above black hole solutions should give rise to a spacetime which is globally uniquely determined. In this talk I will explain how this motivates the study of the wave equation in the interior of black holes, present an overview of previous results, and discuss a recent instability result, obtained in collaboration with Jonathan Luk, in more detail.
Dr. Jessica Lin
University of Wisconsin-Madison
Stochastic Homogenization for Reaction-Diffusion Equations
Monday, December 5, 2016, 5:00pm
Ungar Room 402
Abstract: One way of modeling phenomena in "typical" physical settings is to study PDEs in random environments. The subject of stochastic homogenization is concerned with identifying the asymptotic behavior of solutions to PDEs with random coefficients. Specifically, we are interested in the following: if the random effects are microscopic compared to the lengthscale at which we observe the phenomena, can we predict the behavior which takes place on average? For certain models of PDEs and under suitable hypotheses on the environment, the answer is affirmative. In this talk, I will focus on the stochastic homogenization for reaction-diffusion equations with both KPP and ignition nonlinearities. In the large-scale-large-time limit, the behavior of typical solutions is governed by a simple deterministic Hamilton-Jacobi equation modeling front propagation. Such models are relevant for predicting the evolution of a population or the spread of a fire in a heterogeneous medium. This talk is based on joint work with Andrej Zlatos.
Dr. Verónica Quítalo
CoLab UT Austin-Portugal Program
Systems of Partial Differential Equations Arising from Population Dynamics and Neuroscience:
Free Boundary Problems as a Result of Segregation
Friday, December 2, 2016, 5:00pm
Ungar Room 402
Abstract: In this talk we will motivate and present our recent results on two phase free boundary problems arising from population dynamics. We will focus on systems with fully nonlinear diffusion and local interaction, and linear systems with a (nonlocal) long-range interaction. In the long-range model, the growth of a population at a point is inhibited by the other populations in a full area surrounding that point. This will force the populations to stay at distance one from each other in the limit configuration. So for the first time is obtained a free boundary problem with a gap of no-man's land between the regions where the populations exist. This is a joint work with Luis Caffarelli and Stefania Patrizi.
We will also present briefly some models of differential equations arising from neuroscience and share our current research on propagation of activity in the brain. We will motivate the need to incorporate the "volume" conductivity as well as of the neurons on a model. This is a joint work with Aaron Yip, Zoltan Nadasdy and Silvia Barbeiro.
Dr. Nathan Totz
University of Massachusetts Amherst
Global Flows with Invariant Measures for a Family of Almost Inviscid SQG Equations
Thursday, December 1, 2016, 5:00pm
Ungar Room 402
Abstract: We present a new result, joint with Andrea Nahmod, Natasa Pavlovic, and Gigliola Staffilani, in which very low regularity flows are constructed globally in time almost surely for a family of modified SQG equations using a Gibbs measure; the resulting flows leave this Gibbs measure invariant. The family of equations we treat is formed by adding a small amount of smoothing to the active scalar of the standard inviscid SQG equation. We find that global solutions can be constructed almost surely for any nonzero amount of smoothing.
Dr. Michele Coti-Zelati
University of Maryland
Deterministic and Stochastic Aspects of Fluid Mixing
Monday, November 28, 2016, 5:00pm
Ungar Room 402
Abstract: The process of mixing of a scalar quantity into a homogeneous fluid is a familiar physical phenomenon that we experience daily. In applied mathematics, it is also relevant to the theory of hydrodynamic stability at high Reynolds numbers - a theory that dates back to the 1830's and yet only recently developed in a rigorous mathematical setting. In this context, mixing acts to enhance, in certain senses, the dissipative forces. Moreover, there is also a transfer of information from large length-scales to small length-scales vaguely analogous to, but much simpler than, that which occurs in turbulence. In this talk, we focus on the study of the implications of these fundamental processes in linear settings, with particular emphasis on the long-time dynamics of deterministic systems (in terms of sharp decay estimates) and their stochastic perturbations (in terms of invariant measures).
CANCELLED
Dr. Tye Lidman
North Carolina State University
Left-orderability and Three-manifolds
Friday, October 7, 2016, 4:00pm
Ungar Room 402
Abstract: A group is called left-orderable if it can be given a left-invariant total order. We will discuss the question of when the fundamental group of a three-manifold Y is left-orderable. Orderability is known to be related to certain topological aspects of Y, such as the surfaces which sit inside it. We will discuss a conjectural relationship between left-orderability and the solutions to a certain nonlinear PDE on Y.
CANCELLED
Frank Lutz
Technische Universität Berlin
On the Topology of Steel
Thursday, October 6, 2016, 5:00pm
Ungar Room 402
Abstract: Polycrystalline materials, such as metals, are composed of crystal grains of varying size and shape. Typically, the occurring grain cells have the combinatorial types of 3-dimensional simple polytopes, and together they tile 3-dimensional space.
We will see that some of the occurring grain types are substantially more frequent than others - where the frequent types turn out to be "combinatorially round". Here, the classification of grain types gives us, as an application of combinatorial low-dimensional topology, a new starting point for a topological microstructure analysis of steel.
Ryan Hynd
University of Pennsylvania
Partial Differential Equations in Finance
Thursday, August 25, 2016, 5:00pm
Ungar Room 402
Abstract: Starting with the Black & Scholes equation, I will give a tour of partial differential equations arising in various financial models. My goal is to emphasize what is mathematically interesting about each equation and how solutions are used in applications.
Dr. Daozhou Gao
Shanghai Normal University
The Importance of Synchrony in Mass Drug Administration
Friday, July 8, 2016, 4:30pm
Ungar Room 402
Abstract: Mass drug administration (MDA), a strategy in which all individuals in a population are subject to treatment without individual diagnosis, has been recommended by the World Health Organization for controlling and eliminating several neglected tropical diseases. In this talk, I will present some results arising from mass treatment of trachoma with azithromycin. In the first part, we compare three typical drug distribution strategies (regardless of health status): constant treatment, impulsive synchronized MDA, and impulsive non-synchronized treatment. We show that synchronized and constant strategies are respectively the most and least effective treatments in disease control. Elimination through synchronized treatment is always possible when adequate drug efficacy and coverage is fulfilled and sustained. In the second part, the optimal seasonal timing of mass administration of azithromycin for maximum antimalarial benefit has been established. This is joint work with Thomas M. Lietman and Travis C. Porco.
Dr. Wan-Tong Li
Lanzhou University, China
Nonlocal Effects and Nonlocal Dispersal
Thursday, July 7, 2016, 4:30pm
Ungar Room 402
Abstract: This talk is concerned with some aspects of nonlocal dispersal equations. It consists of three parts. In part one, I will present some relations between local (random) and nonlocal dispersal problems. In part two, I will report our recent results on traveling waves and entire solutions of nonlocal dispersal equations. Part III is devoted to some problems on traveling waves and entire solutions of nonlocal dispersal equations.
Professor Guo Lin
Lanzhou University, China
Traveling Wave Solutions of Evolutionary Models without Monotonicity
Monday, May 9, 2016, 4:00pm
Ungar Room 402
Abstract: This talk is concerned with the traveling wave solutions of evolutionary systems including delayed reaction-diffusion systems and integrodifference equations. Even if the general monotone conditions fail, the existence of traveling wave solutions is studied by generalized upper and lower solutions. The asymptotic behavior is established by the idea of contracting rectangles. In the study of classical Lotka-Volterra competitive systems, we obtain the existence of nonmonotone traveling wave solutions, which weakly confirms the conjecture by Tang and Fife [ARMA, 1980].
Dr. Dmitri Vassiliev
University College London
Spectral Asymptotics for First Order Systems
Thursday, April 14, 2016, 5:00pm
Ungar Room 402
Abstract: In layman's terms a typical problem in this subject area is formulated as follows. Suppose that our universe has finite size but does not have a boundary. An example of such a situation would be a universe in the shape of a 3-dimensional sphere embedded in 4-dimensional Euclidean space. And imagine now that there is only one particle living in this universe, say, a massless neutrino. Then one can address a number of mathematical questions. How does the neutrino field (solution of the massless Dirac equation) propagate as a function of time? What are the eigenvalues (energy levels) of the particle? Are there nontrivial (i.e. without obvious symmetries) special cases when the eigenvalues can be evaluated explicitly? What is the difference between the neutrino (positive energy) and the antineutrino (negative energy)? What is the nature of spin? Why do neutrinos propagate with the speed of light? Why are neutrinos and photons (solutions of the Maxwell system) so different and, yet, so similar?
The speaker will approach the study of first order systems of partial differential equations from the perspective of a spectral theorist using techniques of microlocal analysis and without involving geometry or physics. However, a fascinating feature of the subject is that this purely analytic approach inevitably leads to differential geometric constructions with a strong theoretical physics flavour.
Alexander Volberg
Michigan State University
Rectifiability of Harmonic Measure
Wednesday, April 13, 2016, 4:00pm
Ungar Room 402
Abstract: In a recent multi-authored paper by J. Azzam, S. Hofmann, J.-M. Martell, S. Mayboroda, M. Mourgoglou, X. Tolsa and myself the following result is proved:
For arbitrary open set in any \R^d such that its boundary carries harmonic measure w and for any Borel set $E$, such that $H^{d-1}(E)<\infty, if harmonic measure w|E is absolutely continuous with respect to H^{d-1}|E, then it is rectifiable.
This result solves a long standing conjecture of Chris Bishop and generalizes the result of N. Makarov obtained for d=2 and for simply connected open sets obtained in the early 80's.
We will also make an overview of harmonic measure results of the last 30 years.
Weiyi Zhang
University of Warwick
J-holomorphic Subvarieties
Friday, March 18, 2016, 5:45pm
Ungar Room 402
Abstract: In this talk, we discuss the J-holomorphic subvarieties in a 4-dimensional symplectic manifold. We will start by showing that a subvariety of a complex rational surface in an exceptional rational curve class could have higher genus components. On the other hand, such exotic phenomenon won't happen for (any tamed almost complex structures on) ruled surfaces.
We will then show a general cone theorem as in Mori theory and determine the moduli space of a spherical class in a rational or ruled surface, which could be decomposed as linear systems.
Professor Fedor Bogomolov
New York University
Comparing Torsion Points of Elliptic Curves
Friday, March 18, 2016, 4:45pm
Ungar Room 402
Abstract: In this talk we consider subset of $P^1_{E}\subset P^1$ which are the images of torsion points of complex elliptic curve $E$ under projection defined as a quotient map for standard involution. The corresponding map $E\to P^1$ and hence $P^1_{E}\subset P^1$ is uniquely defined modulo projective transform on $P^1$. It is known that the intersection of subsets $P^1_{E}, P^1_{E'}$ are finite apart from the case when they coincide. However the question is whether there is universal constant bounding this intersection. This problem is somewhat related to Serre conjecture on the image of Galois action on the torsion points. I am going to discuss some results concerning the matter. In particular we show that the intersection contains exactly one point for some families of elliptic curves, that there is an infinite set of pairs $E,E'$ where the intersection consists of $10$ points and also provide a example with $14$ intersection points.
This is joint work with Hang Fu.
Dr. Phillip Griffiths
Institute of Advanced Study, Princeton
University of Miami
The Hodge Conjecture
Friday, February 12, 2016, 5:00pm
Ungar Room 402
Abstract: The Hodge conjecture is one of the Millennium Prize problems. In this talk I will discuss the questions:
• What is it?
• Why is it interesting?
• What is known about it?
• Why has there been almost no progress in solving it?
As little background as possible will be assumed, and what is needed will be informally explained.
Based on joint work with Mark Green, Radu Laza and Colleen Robles.
Ilya Kachkovskiy
University of California, Irvine
Almost Commuting Operators
Tuesday, January 26, 2016, 5:00pm
Ungar Room 402
Abstract: The classical question of whether a pair of matrices or operators with small commutator is close to a commuting pair dates back to von Neumann, Rosenthal, and Halmos. In particular, a dimension-uniform version of this question for Hermitian matrices was open until 1993 when Lin proved the existence of a uniform distance estimate using deep C*-algebraic arguments. Lin's method didn't allow to obtain any quantitative results besides existence. In 2001, Davidson and Szarek conjectured that the distance is bounded by some universal constant times the square root of the norm of the commutator.
In this talk, I will explain the main ideas of the proof of Davidson and Szarek's conjecture (joint work with Y. Safarov), including the infinite-dimensional version.
I will also talk about the relation with Brown-Douglas-Fillmore theorem, and the case of the Hilbert-Schmidt norm for matrices. If time permits, I will discuss some work in progress that includes possible generalization to the case of unitary matrices (where an additional topological obstruction arises), and some applications to mathematical physics.
Dr. Antoine Choffrut
University of Warwick
The Analysis of Partial Differential Equations:
A Case Study with the Euler Equations of Fluid Mechanics
Thursday, January 21, 2016, 5:00pm
Ungar Room 402
Abstract: In this talk I will give an overview of my work on the incompressible Euler equations. It can be categorized in two classes: the use of convex integration to prove h-principles, and structure theorems for two-dimensional stationary flows. These are two very different types of results. However, I will try to highlight a unifying principle in this body of work.
Mihaela Ifrim
University of California, Berkeley
Two Dimensional Water Waves in Holomorphic Coordinates
Thursday, January 14, 2016, 5:00pm
Ungar Room 402
Abstract: This is joint work with Daniel Tataru, and in parts with Benjamin Harrop-Griffits and John Hunter. My talk is concerned with the infinite depth water wave equation in two space dimensions, with either gravity or surface tension. I will also make some remarks on the finite depth case, and on the infinite depth case in which constant vorticity and only gravity are assumed. We consider this problem expressed in position-velocity potential holomorphic coordinates. Viewing this problem(s) as a quasilinear dispersive equation, we develop new methods which will be used to prove enhanced lifespan of solutions and also global solutions for small and localized data. For the gravity water waves there are several results available; they have been recently obtained by Wu, Alazard-Burq-Zuily and Ionescu-Pusateri using different coordinates and methods. In the capillary water waves case, we were the first to establish a global result (two months later, Ionescu-Pusateri also announced a related result). Our goal is improve the understanding of these problems by providing a single setting for all the above cases, and presenting simpler proofs. The talk will try to be self contained.
Mimi Dai
University of Illinois at Chicago
Regularity for the 3D Navier-Stokes Equations and Related Problems
Tuesday, January 12, 2016, 5:00pm
Ungar Room 402
Abstract: As one of the most significant problems in the study of partial differential equations arising in fluid dynamics, Leray's conjecture in 1930's regarding the appearance of singularities for the 3-dimensional (3D) Navier-Stokes equations (NSE) has been neither proved nor disproved. The problems of blow-up have been extensively studied for decades using different techniques. By using a method of wavenumber splitting which originated from Kolmogorov's theory of turbulence, we obtained a new regularity criterion for the 3D NSE. The new criterion improves the classical Prodi-Serrin, Beale-Kato-Majda criteria and their extensions. Related problems, such as the well/ill-posedness, will be discussed as well.
Dr. Eduardo Sontag
Rutgers University
Qualitative Features of Transient Responses
A Case Study: Scale-invariance
Thursday, December 17, 2015, 4:00pm
Ungar Room 402
Abstract: An ubiquitous property of sensory systems is "adaptation": a step increase in stimulus triggers an initial change in a biochemical or physiological response, followed by a more gradual relaxation toward a basal, pre-stimulus level. Adaptation helps maintain essential variables within acceptable bounds and allows organisms to readjust themselves to an optimum and non-saturating sensitivity range when faced with a prolonged change in their environment. It has been recently observed that some adapting systems, ranging from bacterial chemotaxis pathways to signal transduction mechanisms in eukaryotes, enjoy a remarkable additional feature: scale invariance or "fold change detection" meaning that the initial, transient behavior remains approximately the same even when the background signal level is scaled.
I will review the biological phenomenon, and formulate a theoretical framework leading to a general theorem characterizing scale invariant behavior by equivariant actions on sets of vector fields that satisfy appropriate Lie-algebraic non-degeneracy conditions. The theorem allows one to make experimentally testable predictions, and I will discuss the validation of these predictions using genetically engineered bacteria and microfluidic devices, as well their use as a "dynamical phenotype" for model invalidation. I will conclude by briefly engaging in some wild and irresponsible speculation about the role of the shape of transient responses in immune system self/other recognition and in evaluating the initial effects of immunotherapy.
Dr. Phillip Griffiths
Institute of Advanced Study, Princeton
Hodge Theory and Moduli
Wednesday, September 9, 2015, 5:00pm
Ungar Room 402
Abstract: This talk will give an overview of the connection between the above two topics in the first non-classical case of H-surfaces.
Based on joint work with Mark Green, Radu Laza and Colleen Robles.
Professor Wayne Lawton
University of Western Australia
Multivariate Prediction and Spectral Factorization
Thursday, September 3, 2015, 5:00pm
Ungar Room 402
Abstract: Prediction theory studies stationary random functions on ordered groups. Time series are functions on the integer group and characterized by classical harmonic analysis results such as Szego's spectral factorization theorem. Images are functions on higher rank groups. We use results about entire functions and ergodic theory to derive new results for these functions.
Dr. Dimitri Gurevich
Valenciennes University, France
From Quantum Groups to Noncommutative Geometry
Tuesday, May 5, 2015, 4:00pm
Ungar Room 402
Abstract: Since creation theory of Quantum Groups numerous attempts to elaborate an appropriate differential calculus were undertaken. Recently, a new type of Noncommutative Geometry has been obtained on this way. Namely, we have succeeded in introducing the notions of partial derivatives on the enveloping algebras U(gl(m)) and constructing the corresponding de Rham complexes. All objects arising in our approach are deformations of their classical counterparts. In my talk I plan to introduce some basic notions of the theory of Quantum Groups and to exhibit possible applications of thistype Noncommutative Geometry to quantization of certain dynamical models.
Dr. Phillip Griffiths
Institute for Advanced Study, Princeton
Hodge Theory: Some History and a Possible Future Direction
Tuesday, April 21, 2015, 5:00pm
Ungar Room 402
Abstract: Hodge theory is a central part of algebraic geometry. The subject has a long and rich history and continues today to be at the forefront of much current work. This talk will discuss some of its history and one possible, less well known, possible area for future work. In brief: where did the subject come from, and where might it be heading?
Professor Yuval Roichman
Bar-Ilan University
Fine Sets and Schur Positivity
Tuesday, April 14, 2015, 5:00pm
Ungar Room 402
Abstract: Characters of symmetric groups and Iwahori-Hecke algebras may be evaluated by signed (and slightly weighted) enumerations of various classes of permutations, such as conjugacy classes, Knuth classes and inverse descent classes. We propose an abstract framework for such classes, which we call "fine sets".
It will be shown that fine sets can be characterized by Schur positivity of the associated quasi-symmetric functions. The proof involves asymmetric Walsh-Hadamard type matrices. Applications include the equivalence of classical theorems of Lusztig-Stanley and Foata-Schutzenberger.
Time allowing, some very recent developments will be described -- in particular, a generalization to type B and applications to grid classes and derangements, related to results of Desarmenien-Wachs and others.
Based on joint works with R. Adin, C. Athanasiadis and S. Elizalde.
Professor Alexei Kovalev
University of Cambridge
8-dimensional Manifolds with Holonomy Spin(7)
Monday, April 6, 2015, 4:00pm
Ungar Room 402
Abstract: Spin(7) is one of the "exceptional" holonomy groups of Riemannian metrics appearing in Berger's classification. Riemannian manifolds with holonomy Spin(7) occur in dimension 8, are Ricci-flat and have parallel spinor fields. We construct examples of asymptotically cylindrical Riemannian 8-manifolds with holonomy group Spin(7). To our knowledge, these are the first such examples. This leads to a new, connected sum construction of compact holonomy-Spin(7) manifolds from asymptotically cylindrical pairs. We show in examples that the construction produces a "pulling-apart" deformation of compact Spin(7)-manifolds previously given by Joyce, as well as topologically new Spin(7)-manifolds.
Professor Xiuxiong Chen
Stony Brook University
On the Kaehler Ricci Flow
Friday, March 27, 2015, 5:00pm
Ungar Room 402
Abstract: There is a long standing conjecture on Kaehler Ricci flow on Fano manifolds that the Ricci flow converges sub-sequentially to a Kaehler Ricci solution with at most codimension 4 singularities, with perhaps a different complex structure (the so-called "Hamilton-Tian conjecture"). In this lecture, we will outline a proof of this conjecture. This is a joint work with Bing Wang.
Professor Mario Milman
Florida Atlantic University
Uncertainty Inequalities in Metric Measure Spaces
Friday, March 20, 2015, 5:00pm
Ungar Room 402
Abstract: I will show an extension of the classical uncertainty inequalities to connected metric measure spaces. The idea is to exploit the connection with isoperimetry. I will introduce a new class of weights (*isoperimetric weights*) and prove a new local Poincare inequality formulated in terms of the isoperimetric profile. A reinterpretation of the notion of *isoperimetric weights* in terms of function spaces provides a different method to attack the problem and also allows for explicit computation of these weights for log concave measures and other model geometries. I will try to explain all the terms in the abstract, provide examples and show connections with classical inequalities by Hardy and Strichartz.
Professor King-Leung Lam
Ohio State University
On Global Dynamics of Competitive Systems in Ordered Banach Spaces
Tuesday, March 17, 2015, 5:00pm
Ungar Room 402
Abstract: A well-known result in [Hsu-Smith-Waltman, Trans. AMS (1996)] states that in a competitive semiflow defined on the product of two cones in respective Banach spaces, one of the following outcomes is possible for the two competitors: either there is at least one stable coexistence steady state, or else one of the exclusion states attracts all trajectories initiating in the order interval bounded by the two exclusion states. However, none of the exclusion states can be globally asymptotically stable if we broaden our scope to the entire positive cone. In this talk, we discuss two sufficient conditions that guarantee, in the absence of coexistence steady states, the global asymptotic stability of one of the exclusions states. Our results complement the counter example mentioned in the above paper and are frequently applicable in practice.
Dr. Alexander Volberg
Michigan State University
Why the Oracle May Not Exist:
Ergodic Families of Jacobi Matrices,
Absolute Continuity without Almost Periodicity
Thursday, March 5, 2015, 5:00pm
Ungar Room 402
Abstract: We will explain the recent solution of Kotani's problem pertinent to the existence/non-existence of "oracle" (almost periodicity) for the ergodic families of Jacobi matrices (discrete Schroedinger operators). Kotani suggested that such families are subject to the following implication: if family has a non-trivial absolutely continuous spectrum (this happens almost surely) then almost surely it consists of almost periodic matrices (hence the possibility to predict the future by the past). Kotani proved an important positive result of this sort. Recently independently Artur Avila and Peter Yuditskii-myself disproved this conjecture of Kotani (by two different approaches). We will show the hidden singularity that defines when such Kotani's oracle exists or not.
S.R.S. Varadhan
Frank J. Gould Professor of Science
Courant Institute at New York University
Large Deviations for Brownian Occupation Times, Revisited
Friday, February 20, 2015, 5:00pm
Ungar Room 402
Abstract: Brownian motion on R^d is not positive recurrent and the Large Deviation estimate holds only in a weak form. To get a strong version a compactification is needed. In the application of interest we need a translation invariant compactification and that is carried out.
Dr. Lingjiong Zhu
University of Minnesota
Self-Exciting Point Processes
Tuesday, February 17, 2015, 5:00pm
Ungar Room 402
Abstract: Self-exciting point processes are simple point processes that have been widely used in neuroscience, sociology, finance and many other fields. In many contexts, self-exciting point processes can model the complex systems in the real world better than the standard Poisson processes. We will discuss the Hawkes process, the most studied self-exciting point process in the literature. We will talk about the limit theorems and asymptotics in different regimes. Extensions to Hawkes processes and applications to finance will also be discussed.
Dr. Karim Adiprasito
Institute for Advanced Study
Toric Chordality
Monday, February 16, 2015, 5:00pm
Ungar Room 402
Abstract: We put the fundamental graph-theoretic notion of chordality into a proper context within the weight algebra of McMullen and framework rigidity. Moreover, we generalize some of the classical results of graph chordality to this context, including the fundamental relation to the Leray property.
Our main focus is the relation of higher chordality to the Hard-Lefschetz Theorem for simplicial polytopes of Saito, McMullen and others. Homological chordality allows us to state a powerful Quantitative Lower Bound Theorem which relates the "defect" to a chordal complex to the g-numbers of the same polytope, thereby providing an immediate combinatorial interpretation of the g-numbers and, more refinedly, the cohomology classes of the associated projective toric variety, in terms of induced subcomplexes of the simplicial complex. While most of our results follow quite easily once we established stress spaces as the right setting for the study of higher chordality, we provide a central propagation theorem for toric chordality. As an application, we resolve a variety of interesting questions in combinatorics of polytopes.
Dr. Hamed Amini
Swiss Federal Institute of Technology (EPFL), Lausanne
Systemic Risk in Financial Networks
Thursday, February 12, 2015, 5:00pm
Ungar Room 402
Abstract: After the last financial crisis, the monitoring and managing of systemic risk has emerged as one of the most important concerns for regulators, governments and market participants. In this talk, we propose two complementary approaches to modeling systemic risk.
In the first approach, we model the propagation of balance-sheet or cash-flow insolvency across financial institutions as a cascade process on a network representing their mutual exposures. We derive rigorous asymptotic results for the magnitude of contagion in a large financial network and give an analytical expression for the asymptotic fraction of defaults, in terms of network characteristics. We also introduce a criterion for the resilience of a large inhomogeneous financial network to initial shocks that can be used as a tool for monitoring systemic risk. Using an equilibrium approach, in the second part of the talk, we apply a coherent systemic risk measure to examine the effects on systemic risk and liquidation losses of multilateral clearing via a central clearing counterparty (CCP). We provide sufficient conditions in terms of the CCP's fee and guarantee fund policy for a reduction of systemic risk.
Dr. Jin Hyuk Choi
Carnegie Mellon University
Taylor Approximation of Incomplete Radner Equilibrium Models
Tuesday, February 10, 2015, 5:00pm
Ungar Room 402
Abstract: We will first explain the notion of Radner equilibria by using the one-period binomial model. We will see how the complete market assumption simplifies the mathematical structure. In the next part we will consider the setting of exponential investors and uncertainty governed by Brownian motions. Here we will show the existence of an equilibrium for a general class of incomplete models. Finally, we will show that the general incomplete equilibrium can be approximated by a tractable equilibrium stemming from exponential-quadratic models.
Dr. Volker Schlue
University of Toronto
Non-existence of Time-periodic Dynamics in General Relativity
Monday, February 2, 2015, 5:00pm
Ungar Room 402
Abstract: General Relativity presents us with a theory for the dynamics of space and time itself. In this lecture I will revisit the expectation that in contrast to Newton's theory of gravity there does not exist time-periodic motion. In particular, I will present a recent result that establishes purely on the basis of knowing the gravitational waves emitted from any self-gravitating system, that any time-periodic space-time is necessarily "stationary", that is time-independent. Moreover, I will elaborate on novel unique continuation results for hyperbolic partial differential equations that play an important role in the proof, and have been obtained jointly with Spyros Alexakis and Arick Shao.
Dr. Alejandro Morales
University of California, Los Angeles
Matrices over Finite Fields, Polytopes, and Symmetric Functions Related to Rook Placements
Wednesday, January 28, 2015, 5:00pm
Ungar Room 402
Abstract: Permutation matrices are fundamental objects in combinatorics and algebra. Such matrices can be viewed as placements of non-attacking rooks on a square board. If we restrict the support of the matrix we obtain rook placements that in computational complexity are an example of problems where finding a solution is easy but the enumeration is difficult. In this talk we look at various recent results where rook placements appear.
The first instance is counting invertible matrices over a finite field of size q with support that avoids some entries. The number of such matrices is a q-analogue of rook placements but this number may not be a polynomial in q (Stembridge). We give polynomial formulas when the forced zeroes are in the diagonal and on the inversions of some permutations. We also relate the latter to the zoo of combinatorial objects in Postnikov's study of the positive Grassmannian. (Joint works with A. Klein, J. Lewis, R. Liu, G. Panova, S. V Sam, Y. Zhang.)
The second instance is as vertices of the Chan-Robbins-Yuen polytope, a face of the Birkhoff polytope of doubly stochastic matrices. This polytope has a remarkable volume formula proved by Zeilberger. We discuss three variants of this polytope. (Joint works with K. Meszaros, B. Rhoades and J. Striker.)
The third instance is as coefficients in relations among Stanley's chromatic symmetric function and Shareshian-Wachs chromatic quasisymmetric functions on a Catalan family of graphs. (Ongoing work with M. Guay-Paquet and F. Saliola.)
Dr. Antoine Choffrut
University of Edinburgh
Rigidity and Flexibility for the Euler Equations:
The h-principle and the Method of Convex Integration
Tuesday, January 27, 2015, 5:00pm
Ungar Room 402
Abstract: Certain problems in Differential Geometry have long been observed to feature a dichotomy "rigidity vs. flexibility". Rigidity refers to the fact that smooth solutions are unique, while flexibility means that the set of solutions with low regularity can be extremely large. With the groundbreaking work of De Lellis and Szekelyhidi on the incompressible Euler equations of fluid mechanics, it came as an enormous surprise that such a dichotomy may also hold for problems from Mathematical Physics. Flexibility results of interest to us fall under the name of h-principles and are established using the method of convex integration. In this talk I will give a bird's eye view of these notions and explain a motivating conjecture due to Onsager. I will conclude with future problems which deserve special research efforts.
Dr. Angela Hicks
Stanford University
Combining the Classical and the Rational:
Re-expressing Rational Shuffle Conjecture
Friday, January 23, 2015, 5:00pm
Ungar Room 402
Abstract: Recent results have place the classical shuffle conjecture in the context of an infinite family of conjectures about parking functions in any rectangular lattice. The classical case describes three traditional statistics which have varying degrees of complication: area, dinv, and pmaj. Combining the work of many authors in several fields gives two of these statistics in the more general case. After introducing the conjectures, this talk will cover how these statistics can be expressed in a manner consistent with the current classical literature and why this is important. Additionally, this talk will include a conjectured generalization of the third statistic, pmaj, in a number of new cases and time permitting, explain its connection to the sandpile model.
Dr. Nicolas Addington
Duke University
Recent Developments in Rationality of Cubic 4-folds
Tuesday, January 20, 2015, 5:00pm
Ungar Room 402
Abstract: The question of which cubic 4-folds are rational is one of the foremost open problems in algebraic geometry. I'll start by explaining what this means and why it's interesting; then I'll discuss three approaches to solving it (including one developed in the last year), my own work relating the three approaches to one another, and the troubles that have befallen each approach.
Dr. Kristin Shaw
Technical University of Berlin
Tropical Curves and Surfaces
Friday, January 16, 2015, 5:00pm
Ungar Room 402
Abstract: Tropical geometry is a relatively new field of mathematics which provides us with piecewise linear models for classical geometry. Often these models encode properties of the original objects in a more combinatorial form. The first major application of the field to classical geometry came by way of Mikhalkin's correspondence theorem between planar tropical and complex curves. This correspondence has served to answer questions in enumerative geometry; how many curves of a given degree and genus satisfy an appropriate set of constraints? Various other applications have been to moduli problems, linear series on curves, intersection theory, and computations of Hodge numbers. Tropical geometry has also been suggested as a explanation for mirror symmetry.
Abstract tropical varieties in higher dimensions have not been studied to the extend of curves. Applications of tropical geometry to classical geometry often rely on establishing correspondences between the two worlds. In this talk we will see that upon leaving the plane for other surfaces or varieties of higher dimension these correspondences are harder to establish and sometimes do not exist. We will explain how intersection theory and tropical homology can be used to study curves and also tropical Picard groups in surfaces and show how operations known as tropical modification and summation can construct and help study interesting examples of tropical surfaces.
Dr. Morgan Brown
University of Michigan
Rationality of Algebraic Varieties
Thursday, January 15, 2015, 5:00pm
Ungar Room 402
Abstract: An algebraic variety is called rational if it has a parametrization by rational functions which is one-to-one almost everywhere. Determining whether a variety is rational or not is an old and very difficult problem, even when that variety is a smooth hypersurface in projective space. I will give a brief history of this problem, and explain some of the modern techniques for showing that varieties are irrational, including how certain aspects of the derived category might reflect rationality.
Dr. Bruno Benedetti
Free University of Berlin
Diameter of Polytope Graphs
Tuesday, January 13, 2015, 5:00pm
Ungar Room 402
Abstract: "Discrete" geometry focuses on geometric objects that have facets, corners, vertices, rather than on objects with a uniform smooth structure. A standard result is Balinski's theorem, "the graph of every convex d-dimensional polytope is d-connected". But given a d-polytope with n facets, how many edges do we have to walk along (at most), if we want to go from a vertex to another? This "combinatorial diameter" question has relevance in optimization, being related to the simplex algorithm. Hirsch conjectured in 1957 that the answer should be "at most n-d", but the conjecture was disproved by Santos in 2010. I will explain two recent positive results:
(1) The Hirsch conjecture holds for all flag polytopes. The proof uses methods from differential geometry. (Joint work with K. Adiprasito.)
(2) The notion of dual graph naturally extends to projective curves, or to arbitrary algebraic varieties. Surprisingly, a broader version of Balinski's theorem still holds. (Joint work with M. Varbaro, and work in progress with B. Bolognese.)
Dr. Xing Liang
Chinese University of Science and Technology
Spreading Speeds of Monostable Parabolic Equations in Periodic Habitat with Free Boundary
Wednesday, December 17, 2014, 4:30pm
Ungar Room 402
Abstract: In this talk, we will show the existence of the speading speeds of monostable parabolic equations in the spatially and temporally periodic habitats. We main focus on the case where the equations is not linearly determinate.
Dr. James Keesling
Department of Mathematics
University of Florida
An Agent Based Microsimulation Model for the Spread of Citrus Greening
Thursday, November 13, 2014, 5:00pm
Ungar Room 402
Abstract: The citrus industry is a pillar of Florida's economy. It is hard to imagine that it may disappear in short order. However, due to the devastating effects of Citrus Greening, this may very well be the case.
Citrus Greening (or Huang Long Bing) is a disease of citrus caused by a bacterium (Candidatus Liberibacter asiaticus). It is spread by a psyllid, Diaphorina citri. In this talk we will describe a simulation model for the spread of this disease. The model is based on a detailed analysis of the biology of the psyllid vector. Current work expanding and applying the model is being funded by the Citrus Research and Development Foundation as part of the Psyllid Shield Project.
Professor John Stillwell
University of San Francisco
What Does "Depth" Mean in Math?
History, Foundations, and Logic
Thursday, November 6, 2014, 5:00pm
Witten Learning Center 160
Abstract: Every mathematician believes that certain theorems are "deep," but the concept of depth does not have a formal definition. By looking at some famous theorems, ancient and modern, we will study some candidates for "depth" at various levels, particularly the undergraduate level. With these examples in hand we hope to discuss whether any concepts of logic now available can give "depth" a precise meaning.
View Poster
Anatoly Libgober
University of Illinois at Chicago
Landau-Ginzburg/Calabi-Yau and McKay Correspondences for Elliptic Genus
Monday, October 27, 2014, 5:00pm
Ungar Room 506
Abstract: I will discuss elliptic genus of singular varieties and its extension to Witten's phases of N=2 theories. In particular McKay correspondence for elliptic genus will be described. As one of applications I will show how to derive relations between elliptic genera of Calabi-Yau manifolds and related Witten phases using equivariant McKay correspondence for elliptic genus.
Dr. Vyacheslav Shokurov
Johns Hopkins University
Weak Kawamata Conjecture
Wednesday, October 15, 2014, 5:00pm
Ungar Room 506
Abstract: The talk will explain the finiteness of weak log canonical models related by bounded flops.
Dr. Kimihiko Motegi
Nihon University, Tokyo, Japan
Twisted Families of L-space Knots
Wednesday, September 10, 2014, 5:00pm
Ungar Room 402
Abstract: A knot in the 3-sphere is called an L-space knot if it admits a nontrivial Dehn surgery yielding an L-space, which is a generalization of a lens space from the algebraic viewpoint of Heegaard Floer homology. Given an L-space knot K, can we obtain an infinite family of L-space knots by twistings of K along a suitably chosen unknotted circle? We will discuss this question in the case where K admits a Seifert surgery, and give a sufficient condition on such an unknotted circle. If K is a torus knot, then we have an unknotted circle c such that twistings along c produce an infinite family of hyperbolic, L-space knots. In particular, for the trivial knot we can take infinitely many such unknotted circles. We also demonstrate that there are infinitely many hyperbolic, L-space knots with tunnel number greater than one, each of which arises from a trefoil knot by alternate twistings along two unknotted circles.
Dr. Ryan Hynd
Department of Mathematics
University of Pennsylvania
Option Pricing in the Large Risk-aversion, Small-transaction-cost Limit
Thursday, August 21, 2014, 4:00pm
Ungar Room 402
Abstract: We discuss an alternative to the well-known Black-Scholes option pricing model and characterize the asking price of a risk-averse seller, in the limit of small transaction costs. The resulting mathematical problem is one of asymptotic analysis of partial differential equations and the real challenge involves a particular eigenvalue problem.
Professor Andrea Nahmod
University of Massachusetts, Amherst
Randomization and Long Time Dynamics in Nonlinear Evolution PDE
Tuesday, April 29, 2014, 5:00pm
Ungar Room 402
Abstract: The field of nonlinear dispersive equations has undergone significant progress in the last twenty years thanks to the influx of tools and ideas from nonlinear Fourier and harmonic analysis, geometry and analytic number theory, into the existing functional analytic methods. This body of work has primarily focused on deterministic aspects of wave phenomena and answered fundamental questions such as existence and long time behavior of solutions, in various regimes. Yet there remain some important obstacles and open questions.
A natural approach to tackle some of them, and one which has recently seen a growing interest, is to consider certain evolution equations from a non-deterministic point of view (e.g. the random data Cauchy problem, invariant measures, etc.) and incorporate to the deterministic toolbox, powerful but still classical tools from probability as well.
Such approach goes back to seminal work by Bourgain in the mid 90's where global well-posedness of certain periodic Hamiltonian PDEs was studied in the almost sure sense via the existence and invariance of their associated Gibbs measures.
In this talk we will explain these ideas, describe some recent work and future directions with an emphasis on the interplay of deterministic and probabilistic approaches.
Professor Ian Hambleton
McMaster University
Manifolds and Symmetry
Wednesday, April 23, 2014, 5:00pm
Ungar Room 402
Abstract: This will be survey talk about connections between the topology of a manifold and its group of symmetries. I will illustrate this theme by discussing finite group actions on compact manifolds, such as spheres or products of spheres, and infinite discrete groups acting properly discontinuously on non-compact manifolds, such as products of spheres and Euclidean spaces.
Dr. Andras Nemethi
Hungarian Academy of Sciences
Lattice Cohomology and the Geometric Genus of Surface Singularities
Monday, April 14, 2014, 5:00pm
Ungar Room 402
Abstract: The link of a complex normal surface singularity is an oriented 3-manifold. We will review the definition of the lattice cohomology associated with such a plumbed 3-manifold. It makes connection between low-dimensional topology and singularity theory. E.g., its Euler characteristic is the Seiberg-Witten invariant of the link, while in 'nice' cases it also provides the geometric genus of the analytic structure. We will focus on such connections and interplays, together with a historical overview of the topological characterizations of the geometric genus.
Professor Fedor Bogomolov
New York University
On Homomorphisms between Multiplicative Groups of Fields
Wednesday, March 19, 2014, 5:00pm
Ungar Room 402
Abstract: I am going to describe a proof of the theorem which allows for any such homomorphism which respects algebraic dependence between elements is related to a nonarchimedean valuation of the initial field. The only additional condition is that the homomorphism has at least two algebraically independent elements in the image and a nontrivial kernel (not equal to a subfield). This result can be considered as rational version of so called Grothendieck section conjecture for functional fields of transcendence degree greater or equal to two.
Dr. John Shareshian
Washington University
Coset Posets and Probabalistic Zeta Functions of Finite Groups, and a Problem on Binomial Coefficients
Monday, March 17, 2014, 5:00pm
Ungar Room 402
Abstract: Philip Hall introduced the general Möbius inversion formula in order to enumerate the set of k-tuples (g 1,...,g k) from a finite group G that contain a generating set for G. One can substitute an arbitrary complex number, rather than just a positive integer k into the formula obtained by Hall, and the resulting function is called the probabalistic zeta function for G. Serge Bouc observed that evaluation of the probabalistic zeta function at -1 yields the reduced Euler characteristic of a topological space naturally associated to G, namely, the order complex of the poset of all cosets of all proper subgroups of G. Ken Brown investigated this complex and was led to ask whether it is ever contractible. In joint work with Russ Woodroofe, we show that this complex has nontrivial homology, and is therefore not contractible, whenever G has no alternating group as a composition factor. Our efforts to understand alternating composition factors led to a fascinating (at least to me) elementary problem about prime divisors of binomial coefficients.
Dr. Priyanga Amarasekare
UCLA
Temperature Effects on Population Dynamics and Species Interactions:
A Trait-based Perspective
Friday, March 7, 2014, 5:00pm
Ungar Room 402
Abstract: Populations and communities are complex systems whose properties result from the interplay between non-linear feedbacks that are intrinsic to the system (e.g., biotic interactions that lead to density- and frequency-dependence) and external inputs (e.g., abiotic factors) that are outside the feedback structure of the system. Understanding this interplay requires that we understand the mechanisms by which the effects of external inputs on lower levels of the system (e.g., traits of organisms) influence properties at higher levels (e.g., population viability, species diversity). Using temperature as the axis of abiotic variation, I develop a mechanistic theoretical framework for elucidating how abiotic effects on traits influence population dynamics and species interactions, and how these ecological dynamics in turn feedback into the trait response, causing trait evolution. I test model predictions with data on insects. The integration of theory and data paves the way for making testable predictions about the effects of climate warming on population viability, biodiversity and the control of invasive species.
Dr. Gustavo Ponce
UC Santa Barbara
On Unique Continuation Properties of Solutions to Some Dispersive Equations
Thursday, March 6, 2014, 5:00pm
Ungar Room 402
Abstract: We shall discuss results concerning unique continuationproperties of solutions to some canonical dispersive equations and their relation with decay and persistent properties of the corresponding solutions flow. These canonical dispersive models include the generalized Korteweg-de Vries equation, the nonlinear Schrödinger equation and the Benjamin-Ono.
Dr. Emil Wiedemann
PIMS Postdoctoral Fellow
University of British Columbia
Convex Integration for Nonlinear Partial Differential Equations
Tuesday, February 18, 2014, 5:00pm
Ungar Room 402
Abstract: The so-called method of convex integration has been recognized as a powerful tool in various fields of mathematics, including geometry and, more recently, partial differential equations and the calculus of variations. I will discuss the method and two of its recent applications: On the one hand, starting with the recent work of C. De Lellis and L. Szkelyhidi, convex integration methods have been used to construct solutions of equations from fluid dynamics with surprising properties. On the other hand, together with K. Koumatos and F. Rindler, we were able to construct unexpected solutions to first-order equations involving the Jacobian determinant, motivated by questions arising in nonlinear elasticity theory.
Dusa McDuff
Helen Lyttle Kimmel '42 Professor of Mathematics
Barnard College, Columbia University
Symplectic Embeddings in Dimensions 4 and Above
Tuesday, February 11, 2014, 5:00pm
Ungar Room 402
Abstract: Symplectic geometry is a fascinating mix of flexibility and rigidity. One way in which this is shown is in the properties of symplectic embeddings. After explaining what a symplectic structure is, I will describe some recent (and not so recent) results about this question.
Dr. Ting Zhou
C.L.E. Moore Instructor
MIT
On Transformation-Optics Based Invisibility
Monday, January 27, 2014, 5:00pm
Ungar Room 402
Abstract: In this talk, I shall discuss the transformation optics based design of electromagnetic invisible cloaks from the inverse problems point of view. In order to avoid the difficulty posed by the singular structure required for ideal cloaking, we study the regularized approximate cloaking in prototypical models, for time harmonic Maxwell's equations in R 3 and the scalar Helmholtz equations in R 2. In particular, as the regularization parameter converges to zero, i.e., as the approximate cloaking converges to the ideal one, we will see that different types of boundary conditions appearing at the interior of the cloaking interface. Some of them is of non-local pseudo-differential type.
Mihaela Ignatova
Stanford University
On Well-posedness for Free Boundary Fluid-structure Interaction Models
Friday, January 24, 2014, 5:00pm
Ungar Room 402
Abstract: We address a fluid-structure interaction model describing the motion of an elastic body immersed in a viscous incompressible fluid. The model consists of the Navier-Stokes equations (for the fluid) and a linear system of elasticity (for the elastic solid) coupled on the free moving interface via natural dynamic and transmission boundary conditions. We first derive a priori estimates for the local existence of solutions for a class of initial data which also guaranties uniqueness, which leads to the local well-posedness of the model with less regular initial data then previously known. Moreover, under additional interior damping and stabilization terms on the free interface, we prove the global existence and exponential decay of solutions provided the initial data is sufficiently small.
Collaborators: I. Kukavica, I. Lasiecka, and A. Tuffaha
Gregory Pearlstein
Texas A&M University
Singular Metrics and the Hodge Conjecture
Tuesday, January 21, 2014, 5:00pm
Ungar Room 402
Abstract: A Hodge class on a smooth complex projective variety gives rise to an associated hermitian line bundle on a Zariski open subset of a complex projective space P^n. I will discuss recent work with P. Brosnan which shows that the Hodge conjecture is equivalent to the existence of a particular kind of degenerate behavior of this metric near the boundary.
Professor M. Teicher
Bar-Ilan University
Computational Aspects of the Braid Group and Applications
Friday, January 17, 2014, 5:00pm
Ungar Room 402
Abstract: In the talk we will present the 3 most difficult problems in the braid group – "The Word Problem", "The Conjugacy Problem", "The Hurwitz Equivalence Problem" – partial solutions, and applications to cryptography.
Dr. Vedran Sohinger
University of Pennsylvania
On Some Problems Concerning the Nonlinear Schrodinger Equation
Thursday, January 16, 2014, 5:00pm
Ungar Room 402
Abstract: In this talk, we will summarize several recent results concerning the nonlinear Schrodinger equation (NLS). The first part of the talk is dedicated to the study of the low-to-high frequency cascade which occurs as a result of the NLS evolution. In particular, one wants to look at how the frequency support of a solution evolves from the low to the high frequencies. This phenomenon can be quantitatively described as the growth in time of the high Sobolev norms of the solution. We present a method to bound this growth using the idea of an almost conservation law, which was previously used in the low regularity context in the work of Bourgain and Colliander, Keel, Staffilani, Takaoka, and Tao.
In the second part of the talk, we will study the Gross-Pitaevskii hierarchy. This is an infinite system of linear partial differential equations which occurs in the derivation of the nonlinear Schrodinger equation from the dynamics of N-body Bose systems. We will study this hierarchy on the three-dimensional torus. We will show a conditional uniqueness result for the hierarchy in a class of density matrices of regularity strictly greater than 1. Our result builds on the previous study of this problem on R^3 by Erdos, Schlein, and Yau, as well as by Klainerman and Machedon and on the study of this problem on T^2 by Kirkpatrick, Schlein, and Staffilani. Finally, we will apply randomization techniques in order to study randomized forms of the Gross-Pitaevskii hierarchy at low regularities, as was done in the setting of nonlinear dispersive equations starting with the work of Bourgain. The second part of the talk is based on joint work with Philip Gressman and Gigliola Staffilani.
Dr. King-Yeung Lam
Ohio State University
Evolution of Dispersal: A Reaction-Diffusion Approach
Tuesday, January 14, 2014, 5:00pm
Ungar Room 402
Abstract: We consider a reaction-diffusion model of two competing species for the evolution of conditional dispersal in a spatially varying but temporally constant environment. Two species are different only in their dispersal strategies, which are a combination of random dispersal and biased movement upward along the resource gradient. In the absence of biased movement or advection, A. Hastings showed that dispersal is selected against in spatially varying environments. When there is a small amount of biased movement or advection, we show the existence of a positive Evolutionarily Stable Strategy in diffusion rates, which is a form of Nash Equilibrium of the underlying population game.Our analysis of the model suggests that a balanced combination of random and biased movement might be a better habitat selection strategy for populations.
Dr. Dimitri R. Yafaev
University of Rennes, France
Convolutions and Hankel Operators
Monday, December 9, 2013, 5:00pm
Ungar Room 402
Abstract: We compare two classes of integral operators: convolutions in L 2(R) and Hankel operators in L 2(R +). Convolutions have integral kernels b(x - y); they can be standardly diagonalized by the Fourier transform. Hankel operators H can be realized as integral operators with kernels h(t +s). They do not admit an explicit diagonalization. Nevertheless we show that they can be quasi-diagonalized as H = L*ΣL. Here L is the Laplace transform, Σ is the operator of multiplication by a function σ (λ), λ > 0. We find a scale of spaces of test functions where L acts as an isomorphism. Then L* acts as an isomorphism in the corresponding spaces of distributions. We show that h = L* σ which yields an one-to-one correspondence between kernels and sigma-functions of Hankel operators. The sigma-function σ (λ) of a self-adjoint Hankel operator H contains substantial information about its spectral properties. Thus we show that the operators H and Σ have the same numbers of positive and negatives eigenvalues. In particular, we find necessary and sufficient conditions for sign-definiteness of Hankel operators. These results are illustrated at examples of quasi-Carleman operators generalizing the classical Carleman operator with kernel h(t) = t -1 in various directions.
Dr. Dimitri R. Yafaev
University of Rennes, France
Convolutions and Hankel Operators
Monday, December 9, 2013, 5:00pm
Ungar Room 402
Abstract: We compare two classes of integral operators: convolutions in L 2(R) and Hankel operators in L 2(R +). Convolutions have integral kernels b(x - y); they can be standardly diagonalized by the Fourier transform. Hankel operators H can be realized as integral operators with kernels h(t +s). They do not admit an explicit diagonalization. Nevertheless we show that they can be quasi-diagonalized as H = L*ΣL. Here L is the Laplace transform, Σ is the operator of multiplication by a function σ (λ), λ > 0. We find a scale of spaces of test functions where L acts as an isomorphism. Then L* acts as an isomorphism in the corresponding spaces of distributions. We show that h = L* σ which yields an one-to-one correspondence between kernels and sigma-functions of Hankel operators. The sigma-function σ (λ) of a self-adjoint Hankel operator H contains substantial information about its spectral properties. Thus we show that the operators H and Σ have the same numbers of positive and negatives eigenvalues. In particular, we find necessary and sufficient conditions for sign-definiteness of Hankel operators. These results are illustrated at examples of quasi-Carleman operators generalizing the classical Carleman operator with kernel h(t) = t -1 in various directions.
Dr. Erik Lundberg
Purdue University
Statistics on Hilbert's Sixteenth Problem
Tuesday, December 3, 2013, 5:00pm
Ungar Room 402
Abstract: We start with a question motivated by the fundamental theorem of algebra: How many zeros of a random polynomial are real? We discuss three Gaussian ensembles that lead to three different answers. For a polynomial in several variables, the real section of its zero set is much more complicated. Hilbert's sixteenth problem asks to study the possible arrangements of the connected components, and is especially concerned with the case of many components. I will describe a probabilistic approach to studying the topology, volume, and arrangement of the zero set (in real projective space) for a Gaussian ensemble of homogeneous polynomials. We will emphasize a model for random polynomials that is built from a basis of spherical harmonics (eigenfunctions of the spherical Laplacian). This is joint work with Antonio Lerario.
Dr. Paul Kirk
Indiana University, Bloomington
Looking at Knots and 3-manifolds from the Perspective of the Space of Representations of Their Fundamental Group
Friday, November 8, 2013, 4:00pm
Ungar Room 402
Abstract: A fruitful way to study 3-dimensional manifolds, such as the complement of a knot in a 3-sphere, is to study the topological space (algebraic variety) of conjugacy classes of representations of its fundamental group to a Lie group such as SU(2) or SL(2,C). I will describe part of the history and success of this approach, with a focus on illustrating low dimensional examples.
Dr. Gregory Pearlstein
Texas A&M University
Normal Functions and the Hodge Conjecture
Tuesday, September 24, 2013, 5:00pm
Ungar Room 402
Abstract: The theory of normal functions and the Hodge conjecture have their origin in the study of algebraic cycles by Lefschetz and Poincare. I will sketch the history of the subject and discuss some of my recent work on singularities of normal functions to the Hodge conjecture and the zero locus of a normal function to a conjectural filtration of Bloch and Beilinson.
Dr. Shuangjie Peng
Department of Mathematics
Huazhong Normal University, Wuhan, China
On Schrodinger Systems with Nonlinear or Linear Coupling
Tuesday, August 20, 2013, 11:00am
Ungar Room 402
Abstract: We will talk about how to get infinitely many positive non-radial vector solutions which are synchronized or segregated for a Schrodinger system with nonlinear coupling and radially symmetric potentials. We also discuss multiplicity of vector solutions which are segregated for a Schrodinger system with linear coupling.
Dr. Yinbin Deng
Department of Mathematics
Huazhong Normal University, Wuhan China
On the Positive Radial Solutions of a Class of Singular Semilinear Elliptic Equations
Monday, August 19, 2013, 4:00pm
Ungar Room 402
Abstract: In this talk, we are concerned with the following elliptic equation
div ( A(| x|) ∇u) + B(| x|) u p = 0 in R n , (0.1)
where p > 1, n ≥ 3, A(| x|) > 0 is differentiable in R n ¥{0 } and B(| x|) is a given nonnegative Hölder continuous function in R n ¥{0 }. The asymptotic behavior at infinity and structure of separation property of positive radial solutions with different initial data for (0.1) are discussed. Moreover, the existence and separation property of infinitely many positive solutions for Hardy equation and an equation related to Caffarelli-Kohn-Nirenberg inequality are obtained respectively, as special cases.
Professor Erwan Rousseau
LATP CMI Aix-Marseille University
Complex Hyperbolicity, Differential Equations and Automorphic Forms
Wednesday, April 24, 2013, 4:00pm
Ungar Room 402
Abstract: I will explain how the study of entire curves in complex projective manifolds is related to differential equations and automorphic forms.
Dr. Mu-Tao Wang
Columbia University
A Minkowski Inequality and a Penrose Inequality
Friday, April 5, 2013, 5:00pm
Ungar Room 402
Abstract: The classical inequality of Minkowski relates the total mean curvature of a convex surface to the area of the surface. I shall discuss a newly discovered Minkowski type inequality which can be interpreted as the Penrose inequality for collapsing shells in general relativity. This is joint work with Simon Brendle and Pei-Ken Hung.
Persi Diaconis
Mary V. Sunseri Professor of Statistics and Mathematics
Stanford University
Shuffling Cards, Breaking Rocks and Hopf Algebras
Friday, March 29, 2013, 5:00pm
Ungar Room 402
NOTE: Professor Diaconis will also be delivering the McKnight-Zame Distinguished Lecture on Wednesday, March 27.
Abstract: Hopf algebras are combinatorial objects introduced by topologists to study the topology of classical groups. In joint work with Amy Pang and Arun Ram, we show that the Hopf square map (coproduct followed by product) often has a simple probabilistic interpretation. It allows us to explicitly diagonalize well-known Markov chains: the classical model of riffle shuffling cards and a rock breaking model of Kolmogorov among others. I will try to present all of this in mathematical English, explaining all the words above.
Susan Holmes
Professor of Statistics
Stanford University
Mathematical and Statistical Approaches to Heterogeneous Data:
Challenges from the Human Microbiome
Thursday, March 28, 2013, 5:00pm
Ungar Room 402
Abstract: Through new sequencing technologies, we can make a census of the bacteria living in the human gut. We also have phylogenetic information about the taxa present and clinical information about the subjects. Distance based methods allow us to create useful representations integrating all this data and make useful visualizations that allow us to discover bacterial markers for disease and follow the dynamics of the bacterial communities.
This is joint work with David Relman and his Stanford Lab.
Dr. Richard Stanley
Norman Levinson Professor of Applied Mathematics
Massachusetts Institute of Technology
Polynomial Sequences of Binomial Type
Tuesday, January 15, 2013, 5:00pm
Ungar Room 402

Mihalis Dafermos
Professor of Mathematical Physics
Cambridge University
A Scattering Theory Construction of Dynamical Black Holes
Wednesday, December 19, 2012, 4:00pm
Ungar Room 402
Dr. Joshua Greene
Boston College
Dehn Surgery and Floer Homology
Thursday, November 29, 2012, 5:00pm
Ungar Room 402
Abstract: Dehn surgery is a natural operation occurring in low-dimensional topology. It gives a method to create 3-manifolds out of knots and links, and there are many very attractive results and problems about it. One central problem is the Berge conjecture, which predicts when Dehn surgery along a knot in the three-sphere can produce a lens space. Floer homology has played a prominent role in low-dimensional topology during the past twenty-five years. It developed out of gauge theory and symplectic geometry, and one of its versions associates invariants to 3-manifolds and other objects in low-dimensional topology. I will discuss the central role that Floer homology has played in the study of Dehn surgery, and in particular what it tells us about the Berge conjecture.
CANCELLED
Dr. Eugene Gorsky
Stony Brook University
Compactified Jacobians, q,t-Catalan Numbers and Knot Invariants
Thursday, November 1, 2012, 5:00pm
Ungar Room 402
Abstract: Campillo, Delgado and Gusein-Zade proved that the semigroup of a plane curve singularity encodes the information about the Alexander polynomial of its link. Oblomkov and Shende conjectured an extension of their result to to the HOMFLY polynomial, which uses the Hilbert schemes and compactified Jacobians of a singular curve. I will explain the combinatorics of their construction in the simplest example of torus knots, and relate it to the generalization of q,t-Catalan numbers of Garsia and Haiman. The talk is based on joint work with M. Mazin.
Dr. Fernando Schwartz
University of Tennessee
Geometric Inequalities for Hypersurfaces
Thursday, October 11, 2012, 5:00pm
Ungar Room 402
Abstract: We revisit some classic estimates for the capacity as well as a version of the Alexandrov-Fenchel inequality for hypersurfaces of Euclidean space. We provide new, more general proofs of these inequalities, and include some rigidity statements. The results are joint work with Alexandre Freire.
Professor Lars Andersson
Albert Einstein Institute
Max Planck Institute for Gravitational Physics
Cosmological Models and Stability
Thursday, October 4, 2012, 5:00pm
Ungar Room 402
Abstract: In this talk I will discuss some mathematical results on inhomogeneous cosmological models, focusing on late time behavior and the issues of nonlinear stability versus instability.
Professor Fernando Coda Marques
IMPA, Brazil
Min-max Minimal Surfaces and the Willmore Conjecture
Monday, April 30, 2012, 4:00pm
Ungar Room 402
Abstract: In 1965, T. J. Willmore conjectured that the integral of the square of the mean curvature of a torus immersed in Euclidean three-space is at least 2π 2 . In this talk we will discuss a proof of this conjecture that uses the min-max theory of minimal surfaces. This is a joint work with Andre Neves of Imperial College (UK).
Professor Ernesto Lupercio
Center for Research and Advanced Studies of the
National Polytechnic Institute (Cinvestav-IPN)
Virtual Orbifold Cohomology
Wednesday, April 25, 2012, 4:00pm
Ungar Room 402
Abstract: In this talk of a mostly expository nature I will explain the orbifolding procedure for topological field theories and a new family of examples. I will first introduce the concept of topological field theory and orbifold. This is joint with Gonzalez, Segovia, and Uribe.
Dr. Sebastian Schreiber
University of California, Davis
Should I Stay or Should I Go?
An SDE Perspective on the Ecology and Evolution of Movement
Friday, March 30, 2012, 5:00pm
Ungar Room 402
Abstract: All populations, whether they be plants, animals, or viruses, live in spatially and temporally variable environments. Understanding how this variability influences population persistence and the evolution of movement is a fundamental issue of practical and theoretical importance in population biology. Prior work (including important contributions due to Chris Cosner and Steve Cantrell) has shown that spatial variability, in and of itself, enhances persistence and selects against random movement as well as movement into sink habitats (places unable to harbor a self-sustaining population). Alternatively, temporal variability, in and of itself, inhibits persistence and exerts no selective pressures on movement. The combined effects, however, of spatial and temporal variability are remarkably complex. This combined variability can select for movement into sink habitats and allow for populations to persist in landscapes comprised solely of sink habitats. In this talk, I will discuss recent analytic results in which populations living in patchy environments are modeled using stochastic differential equations (SDEs). These results provide a diversity of new insights into population persistence and the evolution of movement. Part of this work was done in collaboration with Steve Evans (Berkeley), Peter Ralph (Davis), and Arnab Sen (Cambridge).
Dr. Ryan Derby-Talbot
Quest University
Are Complicated 3-manifolds Complicated?
Thursday, March 29, 2012, 5:00pm
Ungar Room 402
Abstract: In this talk we will discuss several ways that one can construct 3-manifolds (shapes like our spatial universe), and various ways that these constructions can be made complicated. Surprisingly, a 3-manifold made complicated by one construction may actually be simple in another construction, and necessarily so. We will explore different ways that complicating 3-manifolds in some ways simplifies them in others. Lots of fun pictures are promised.
Professor Lars Andersson
Albert Einstein Institute
Max Planck Institute for Gravitational Physics
Hidden Symmetries and Conserved Charges
Monday, March 12, 2012, 4:00pm
Ungar Room 402
Abstract: Test fields with non-zero spin, eg. Maxwell and linearized gravity provide an important model problem for black hole stability. Fields with non-zero spin admit non-radiating modes which must be eliminated in order to prove decay. In this talk I will discuss the relation between conserved charges and hidden symmetries for linearized gravity on Minkowski space and vacuum spaces of Petrov type D and outline the application of these ideas in proving estimates for the higher spin fields on the Kerr background.
Dr. Andras Stipsicz
Renyi Institute of Mathematics (Budapest)
Institute for Advanced Study (Princeton)
Computations of Heegaard Floer Homologies
Friday, March 9, 2012, 4:00pm
Ungar Room 402
Abstract: Heegaard Floer homology groups were recently introduced by Ozsvath and Szabo to study properties of 3-manifolds and knots in them. The definition of the invariants rests on delicate holomorphic geometry, making the actual computations cumbersome. In the lecture we will recall the basic definitions and theorems of the theory, and show how to define the simplest version in a purely combinatorial manner. For a special class of 3-manifolds the more general version will be presented by simple combinatorial ideas through lattice homology of Nemethi.
CANCELLED
Professor Ross Pinsky
Technion – Israel Institute of Technology
Probabilistic and Combinatorial Aspects of the Card-Cyclic to Random Insertion Shuffle
Tuesday, March 6, 2012, 5:00pm
Ungar Room 402
Abstract: Consider a permutation σ j ∈ S n as a deck of cards numbered from 1 to n and laid out in a row, where σ j denotes the number of the card that is in the j-th position from the left. We study some probabilistic and combinatorial aspects of the shuffle on S n defined by removing and then randomly reinserting each of the n cards once, with the removal and reinsertion being performed according to the original left to right order of the cards. The novelty here in this nonstandard shuffle is that every card is removed and reinserted exactly once. The bias that remains turns out to be quite strong and possesses some surprising features.
Dr. Carmen Coll
Instituto de Matematica Multidisciplinar
Universidad Politecnica de Valencia
Valencia, Spain
ITME Visiting Scholar
Identifiability of Parameters for Structured Systems
Monday, February 27, 2012, 3:30pm
Ungar Room 402
Abstract: Mathematical models have been successfully developed to study real processes. Usually, the situation is as follows: the inputs, u, can be controlled, the outputs, y, can be observed, but the description of what happens inside is not unknown. This situation is called the input-output behavior of the system.
In general, the state-space representation of these processes involves coefficient matrices and the equations of the model have unknown parameters that can be determined from experimental data. A good formulation of the model is essential because this fact allows us to predict or control the behavior of the real process. Moreover, it can be used to estimate quantities that cannot be measured directly from observations. In this case, it is useful to obtain these parameters to accurate the model. The problem of identifying the unknown parameters within the model uniquely from the experiment considered is called the identifiability problem. That is, a system is identifiable if the relationship between the set of possible parameter values and the set of possible input-output behaviors is one-to-one.
On the other hand, many of these models have a fixed structure and we want to solve the identifiability problem when this structured holds on. The structural identifiability analysis of a system is a preliminary analysis of the model structure oriented to the parameter and model identification. The problem of the structural identifiability of the model consists of the determination of all parameter sets which give the same input-output structure.
In this talk, parametric systems with different matrix structures are considered. The structural properties of the model are studied, and some conditions to assure the structural identifiability are given. These results guarantee the existence of only one solution for the parameters of the system. In practice, systems with one of these structures arise, for example, via discretization or finite difference methods for solving boundary and initial value problems involving differential or partial differential equations.
Dr. Huaiping Zhu
York University
Forecasting Mosquito Abundance and West Nile Virus Risk Using Weather and Environment Conditions
Friday, February 24, 2012, 5:00pm
Ungar Room 402
Abstract: It has been witnessed for the last decades that climate change has great impact on the emerging and reemerging of vector-borne diseases, yet it must be admitted that the actual impact of climate change on vector population and diseases transmission are still far from clear. In this talk, I will present a modeling study of the West Nile virus in the Peel region of Ontario, Canada. By using surveillance data, weather data and land use information, we develop both statistical and dynamical models incorporating weather conditions and land use information for the vector-mosquitoes abundance and risk assessment of West Nile virus. I will discuss the statistical properties of the dynamical models and present a collaborative effort with Peel region and Public Health Agency of Canada in developing tools for forecasting the mosquito-abundance and the virus risk.
Dr. Lev Ginzburg
Department of Ecology and Evolution
Stony Brook University
Life is 4D: Allometric Slopes Are Understandable when Viewed in 4D
Monday, February 6, 2012, 3:30pm
Ungar Room 402
Professor Roger Arditi
Department of Ecology and Evolution
Université Pierre et Marie Curie, Paris
How Species Interact
Friday, February 3, 2012, 5:00pm
Ungar Room 402
Abstract: Understanding the functioning of ecosystems requires the understanding of the interactions between consumer species and their resources. How do these interactions affect the variations of population abundances? How do population abundances determine the impact of predators on their prey? The authors defend the view that the "null model" that most ecologists tend to use (derived from the Lotka-Volterra equations) is inappropriate because it assumes that the amount of prey consumed by each predator is insensitive to the number of conspecifics. The authors argue that the amount of prey available per predator (rather than the absolute abundance of prey) is the basic determinant of the dynamics of predation. This so-called ratio dependence is shown to be a much more reasonable "null model". Lessons can be drawn from a similar debate that took place in microbiology in the 1950's. Currently, populations of bacteria are known to follow the analogue of ratio dependence when growing in real-life conditions. Three kinds of arguments are developed. First, it is shown that available direct measurements of prey consumption are "in the middle" but most are close to ratio dependence and all are clearly away from the usual Lotka-Volterra relationship; an example is the system of wolves and moose on Isle Royale. Second, indirect evidence is based on the responses of food chains to nutrient enrichment: all empirical observations at the community level agree very well with the ratio-dependent view. Third, mechanistic approaches explain how ratio dependence emerges at the global scale, even when assuming Lotka-Volterra interactions at the local scale; this is illustrated by microcosm experiments, by individual-based models and by mathematical models. Changing the fundamental paradigm of the predator-prey interaction has far-reaching consequences, ranging from the logical consistency of theoretical ecology to practical questions of eco-manipulation, biological control, conservation ecology.
This work is in collaboration with Lev Ginzburg.
Professor Larry Shepp
Patrick T. Harker Professor
Wharton School, University of Pennsylvania
Board of Governor's Professor
Rutgers University
Is Mathematical Modeling Able to Give Insight into Current Questions in Finance, Economics, and Politics?
Thursday, February 2, 2012, 5:00pm
Ungar Room 402
Abstract: Part I. I argue that rigorous mathematics gives insight into the current question of whether taxation helps or hinders employment.
Part II. I compute (within one simple model) how much money future knowledge, obtained either via insider information or via high-frequency trading, of future stock prices brings to a possessor of such knowledge.
Professor Sergiu Klainerman
Higgins Professor of Mathematics
Princeton University
On the Bounded L 2 Curvature Conjecture as a Breakdown Criteria for the Einstein Vacuum Equations
Wednesday, January 11, 2012, 4:00pm
Ungar Room 402
Abstract: I will talk about my recent work with Rodnianski and Szeftel concerning a solution of the conjecture. I will also compare the result with the other known breakdown criteria in GR.
Dr. Michael Eichmair
Massachusetts Institute of Technology
Isoperimetric Structure of Initial Data Sets
Friday, December 16, 2011, 4:00pm
Ungar Room 402
Abstract: I will present joint work with Jan Metzger. A basic question in mathematical relativity is how geometric properties of an asymptotically flat manifold (or initial data set) encode information about the physical properties of the space time that it is embedded in. For example, the square root of the area of the outermost minimal surface of an initial data with non-negative scalar curvature provides a lower bound for the "mass" of its associated space time, as was conjectured by Penrose and proven by Bray and Huisken-Ilmanen. Other special surfaces that have been studied in this context include stable constant mean curvature surfaces and isoperimetric surfaces. I will explain why positive mass works to the effect that large stable constant mean curvature surfaces are always isoperimetric. This answers an old conjecture of Bray's and complements the results by Huisken-Yau and Qing-Tian on the "global uniqueness problem for stable CMC surfaces" in initial data sets with positive scalar curvature. Time permitting, I will sketch applications related to G. Huisken's isoperimetric mass and very recent related results with S. Brendle on further isoperimetric features of the exact spatial Schwarzschild metric.
Dr. Martin Bootsma
Department of Mathematics
Utrecht University, The Netherlands
The Spreading Capacity of Methicillin-resistant Staphylococcus aureus (MRSA)
Tuesday, December 6, 2011, 5:00pm
Ungar Room 402
Abstract: In my talk I will discuss an example of cross-fertilization between medicine and mathematics. Data on the size of outbreaks with methicillin-resistant Staphylococcus aureus (MRSA) in Dutch hospitals were collected to estimate the transmissibility of the two most relevant MRSA strains in the Netherlands. Analysis of these data led to a relation between the epidemiological model for the spread of MRSA in hospitals and queuing theory, and a new estimation method for transmissibility of pathogens in outbreak settings with contact screening. In very recent theoretical work, Amaury Lambert and Pieter Trapman derive an improved estimator if easily collectable data is available. These data are now collected in a currently performed study in the Netherlands.
Dr. Pierre Magal
University of Bordeaux Segalen, France
P-gp Transfer and Acquired Multi-drug Resistance in Tumors Cells
Monday, November 28, 2011, 4:30pm
Ungar Room 402
Abstract: Multi-drug resistance for cancer cells as been a serious issue since several decades. In the past, many models have been proposed to describe this problem. These models use a discrete structured for the cancer cell population, and they may include some class of resistant, non resistant, and acquired resistant cells. Recently, this problem has received a more detailed biological description, and it turns out that the resistance to treatments is due in 40% of cancers to a protein called P-glycoprotein (P-gp). Moreover some new biological experiments show that transfers can occur by the mean of Tunneling nanoTubes built in between cells (direct transfers). Transfers can also occur through microparticles (containing P-pg) released by over expressing cells into the liquid surrounding these cells. These microparticles can then diffuse and can be recaptured by the cells (indirect transfers). This transfers turn to be responsible for the acquired resistance of sensitive cells. The goal of this talk is to introduce this problem, and to present a cell population dynamic model with continuous P-gp structure.
Professor DaGang Yang
Tulane University
Einstein 4-Manifolds with Pinched Sectional Curvature
Thursday, November 17, 2011, 5:00pm
Ungar Room 402
Abstract: Let (M, g) be a compact, simply connected n-dimensional Riemannian manifold with sectional curvature K. (M, g) is said to be pointwise ε-pinched for some constant 1 ≥ ε > 0 if there is a positive function K 0 on M such that K 0 ≥ K > εK 0 .
Question: For what values of ε, can one expect the Ricci flow initiated from g to converge to a metric of constant sectional curvature, and therefore diffeomorphic to the standard sphere S n ?
The 1/4-pinched differentiable sphere theorem, by H.W. Chen for n = 4, and by S. Brendle and R. M. Schoen for n ≥ 5, says that ε = 1/4 is the smallest possible value. For ε < 1/4, P. Petersen and T. Tao have shown that there is a constant ε n , 1/4 > ε n > 0 , for each dimension n such that, if 1 ≥ K > ε n , then the Ricci flow initiated from g will converge to a metric which is either of constant sectional curvature or is a compact rank one symmetric space.
It is therefore natural to propose the following question: For each n ≥ 4, what is the smallest pinching constant ε n > 0 such that, if K 0 ≥ K > ε nK 0 , then the Ricci flow initiated from g can still be expected to converge to a metric of constant sectional curvature or to a metric of a compact rank one symmetric space?
In other words, are there any other models of Einstein manifolds with pinched positive sectional curvature in each dimension n ≥ 4?
In this talk, I shall discuss some old and new results in this area for n=4.
Dr. Jan Medlock
Clemson University
Issues in the Ecology and Evolution of Dengue
Friday, April 8, 2011, 5:00pm
Ungar Room 402
Abstract: Dengue is a mosquito-borne viral pathogen that causes large amounts of disease in the tropics and sub-tropics. Dengue viruses are divided into four large clades, called serotypes: infection with a virus produces complete immunity to viruses within that same serotype, but increases the risk of severe disease upon infection with a virus from a different serotype. Multiple mechanisms have been hypothesized for this interaction between serotypes in the human immune system, which, combined with seasonal oscillations in mosquito abundances, lead to complex behavior in mathematical models. In addition, two new interventions for dengue are currently in intense development: a vaccine that protects against all four serotypes and transgenic mosquitoes that are less-suitable vectors. In this talk, I will discuss a model for evolution of dengue viruses in response to these new interventions and work in progress on the best population groups to target with vaccine to minimize disease burden.
Dr. Jim Haglund
University of Pennsylvania
Macdonald Polynomials and the Hilbert Series of the Quotient Ring of Diagonal Coinvariants
Thursday, April 7, 2011, 5:00pm
Ungar Room 402
Abstract: Macdonald polynomials are symmetric functions in a set of variables X which also depend on two parameters q,t. In this talk we describe how a formula of Haiman for the Hilbert series of the quotient ring of diagonal coinvariants in terms of Macdonald polynomials implies a much simpler expression for the Hilbert series involving matrices satisfying certain constraints.
Dr. Marcus Khuri
Stony Brook University
The Positive Mass Theorem with Charge Revisited
Thursday, March 31, 2011, 5:00pm
Ungar Room 402
Abstract: In the early 80's Hawking et al. generalized the positive mass theorem to include charge. It was conjectured that the case of equality should occur only for the extremal black hole solutions known as Majumdar-Papapetrou spacetimes. Chrusciel et al. confirmed this under extra assumptions. In this talk we will show how these extra hypotheses may be removed. This is joint work with Gilbert Weinstein.
Richard P. Stanley
Norman Levinson Professor of Applied Mathematics
Massachusetts Institute of Technology
A Survey of Alternating Permutations
Tuesday, March 22, 2011, 5:00pm
Ungar Room 402
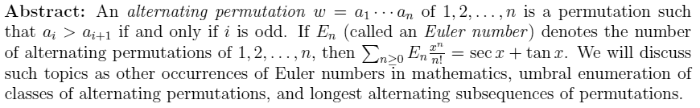
Professor Xiaodong Wang
Michigan State University
Volume Entropy and Ricci Curvature
Thursday, March 10, 2011, 5:00pm
Ungar Room 402
Abstract: The volume entropy is a very interesting invariant of a Riemannian manifold. When the Ricci curvature has a negative lower bound, there is a sharp lower bound for the volume entropy. I will discuss why the equality case characterizes hyperbolic manifolds. In certain cases, we can also prove that the manifold is close to a hyperbolic manifold in the Gromov-Hausdorff sense if the volume entropy is close to the sharp lower bound. The method involves the Busemann compactification and Patterson-Sullivan measure. This is a joint work with Francois Ledrappier.
Dr. David Smith
University of Florida
and
Center for Disease Dynamics Economics and Policy Washington, DC
Recasting the Theory of Transmission by Mosquitoes
Thursday, February 24, 2011, 5:00pm
Ungar Room 402
Abstract: Mathematical modeling for mosquito-borne diseases has been used to develop theory and guide disease control for more than a century, but the demands on models have been changing. Analysis of a comprehensive review of mosquito-borne transmission models demonstrated that mosquito-borne disease models follow the conventions of the Ross-Macdonald model and that there has been little innovation in modeling transmission. A new mathematical description of transmission was based on mosquito movement, aquatic ecology and blood feeding behavior. Mosquito movement can be described concisely as a random walk on a bipartite graph. Transmission also depends on the ways that mosquitos allocate bites on humans and the way humans allocate their time at risk. This framework provides a starting point for reformulating a new theory of transmission that captures other aspects of mosquito behavior that are important for transmission but absent from the Ross-Macdonald model.
Dr. Xinzhi Liu
Department of Applied Mathematics
University of Waterloo
Waterloo, Canada
Epidemic Models with Switching Parameters
Wednesday, February 23, 2011, 5:00pm
Ungar Room 402
Abstract: Epidemic models are vital for implementing, evaluating, and optimizing control schemes in order to eradicate a disease. These mathematical models may be oversimplified, but they are useful for gaining knowledge of the underlying mechanics driving the spread of a disease, and for estimating the number of vaccinations required to eradicate a disease. This talk discusses some epidemic models with switching parameters. Both constant control and pulse control schemes are examined, and, in doing so, we hope to gain insight into the effects of a time-varying contact rate on critical control levels required for eradication.
Professor Tatiana Toro
University of Washington
Potential Theory Meets Geometric Measure Theory
Tuesday, February 22, 2011, 5:00pm
Ungar Room 402
Abstract: A central question in Potential Theory is the extent to which the geometry of a domain influences the boundary regularity of solutions to divergence form elliptic operators. To answer this question one studies the properties of the corresponding elliptic measure. On the other hand one of the central questions in Geometric Measure Theory (GMT) is the extent to which the regularity of a measure determines the geometry of its support. The goal of this talk is to present a few instances in which techniques from GMT and Harmonic Analysis come together to produce new results in both of these areas.
Professor Ernesto Lupercio
Research and Advanced Studies Center of the
National Polytechnic Institute of Mexico (Cinvestav-IPN)
Winner of the 2009 Srinivasa Ramanujan Prize
The Moduli Space of (Non-commutative) Toric Varieties
Friday, February 18, 2011, 4:30pm
Ungar Room 402
Abstract: In this talk I will describe my work in progress with Laurent Meersseman and Alberto Verjovvsky on the moduli space of Toric Manifolds. Using specific families of foliations and the Gale transform we describe some basic geometric and topological properties of this moduli space.
Professor Herbert S. Wilf
Thomas A. Scott Emeritus Professor of Mathematics
University of Pennsylvania
There's Plenty of Time for Evolution
Thursday, February 17, 2011, 2:00pm
Ungar Room 402
Abstract: Those who are skeptical of the Darwinian view of evolution often argue that since there are K^n possible n letter words over a K letter alphabet, it must take an exponentially long time before random mutations of the letters will produce "the right word." We show that if the effects of natural selection are taken into account in a reasonable way, the K^n time estimate can be replaced by Kn log n. As a byproduct we obtain the mean of the largest of many geometrically distributed random variables. This is joint work with Warren Ewens.
Dr. Nathan Geer
Utah State University
The Colored Jones Polynomial and Some of Its Relatives
Tuesday, February 15, 2011, 5:00pm
Ungar Room 402
Abstract: In this talk I will discuss a problem in quantum topology called the Volume Conjecture. This conjecture relates the colored Jones polynomials with the hyperbolic volume of the knot complement. As I will explain the Volume Conjecture links together elements of topology, geometry and algebra. I will begin with a gentle introduction to knot theory and the definition of the Jones polynomial. Then I will show how to compute the colored Jones polynomial using algebra. Finally after stating the conjecture, I will discuss some related topological invariants.
Professor Larry Shepp
Wharton School, University of Pennsylvania
and
Rutgers University
Some New Probability Problems; Some New Solutions
Thursday, February 10, 2011, 5:00pm
Ungar Room 402
Abstract: I will first update the situation discussed last year re the artificial pancreas project. The problem is now to upgrade the sensor by getting a better algorithm for recalibration. This is a really important and beautiful problem. I will tell you about my recent work on it; it's still very open.
The second update is a beautiful theoretical problem recently posed by Mike Steele. The problem is this: consider a sequence of n iid uniform variables on [0,1]. Call a subsequence "upsy-downsy", if no three successive terms of the subsequence are monotonic. It is known (Houdre-Stanley-Widom) that if one can search all subsequences, then the expected length of the longest upsy-downsy subsequence is asymptotic to n times 2/3. Steele asked a question of interest to people in stochastic optimization: what is the length of the upsy-downsy subsequence if each term is optimally chosen, {\em without knowing the rest of the sequence, as in the famous secretary problem. We showed the answer is asymptotic to n times c, where c = 2 - \sqrt{2} = .586\ldots < 2/3$. I will indicate two approaches to this problem, each of which gives the right answer, but only one of which I regard as mathematically legitimate.
Dr. Slawomir Kwasik
Tulane University
Souls of Manifolds via Curvature and Surgery
Thursday, January 27, 2011, 5:00pm
Ungar Room 402
Abstract: Deep connections between topology and geometry will be discussed in the case of manifolds with non-negative (sectional) curvature. Historical perspective of these connections and new developments will be presented.
Dr. Chuan Xue
Mathematical Biosciences Institute at Ohio State
A Mathematical Model of Chronic Wounds
Thursday, January 20, 2011, 5:00pm
Ungar Room 402
Abstract: Chronic wound healing is a staggering public health problem, affecting 6.5 million individuals annually in the U.S. Ischemia, caused primarily by peripheral artery diseases, represents a major complicating factor in the healing process. In this talk, I will present a mathematical model of chronic wounds that represents the wounded tissue as a quasi-stationary Maxwell material, and incorporates the major biological processes involved in the wound closure. The model was formulated in terms of a system of partial differential equations with the surface of the open wound as a free boundary. Simulations of the model demonstrate how oxygen deficiency caused by ischemia limit macrophage recruitment to the wound-site and impair wound closure. The results are in tight agreement with recent experimental findings in a porcine model. I will also show analytical results of the model on the large-time asymptotic behavior of the free boundary under different ischemic conditions of the wound.
Dr. Valerie Hower
University of California, Berkeley
A Shape-based Method for Determining Protein Binding Sites in a Genome
Tuesday, January 18, 2011, 5:00pm
Ungar Room 402
Abstract: We present a new algorithm for the identification of bound regions from ChIP-Seq experiments. ChIP-Seq is a relatively new assay for measuring the interactions of proteins with DNA. The binding sites for a given protein in a genome are "peaks" in the data, which is given by an integer-valued height function defined on the genome. Our method for identifying statistically significant peaks is inspired by the notion of persistence in topological data analysis and provides a non-parametric approach that is robust to noise in experiments. Specifically, our method reduces the peak calling problem to the study of tree-based statistics derived from the data. The software T-PIC (Tree shape Peak Identification for ChIP-Seq) is available at http://math.berkeley.edu/~vhower/tpic.html and provides a fast and accurate solution for ChIP-Seq peak finding.
Dr. Peter Kim
University of Utah
Imatinib Dynamics and Cancer Vaccines:
From Agent-Based Models to PDEs
Thursday, January 13, 2011, 5:00pm
Ungar Room 402
Abstract: Various models exist for the interaction between the drug imatinib and chronic myelogenous leukemia. However, the role of the immune response during imatinib treatment remains unclear. Based on experimental data, we hypothesize that imatinib gives rise to a brief anti-leukemia immune response as patients enter remission.
We propose that cancer vaccinations during imatinib treatment can boost the existing immune response and lead to a sustained remission or a potential cure. To examine this hypothesis, we take a model by Michor et al. and extend it to a delay differential equation (DDE) model by incorporating an anti-leukemia immune response. We show that properly-timed vaccines can sustain the immune response to potentially prolong remission or eliminate cancer.
For comparison, we analyze an agent-based model developed independently by Roeder et al. We develop a partial differential equation (PDE) model that captures the same behavior as the Roeder agent-based model and extend it by incorporating an immune response. We conclude that both the DDE and PDE models exhibit similar behaviors with regard to cancer remission, implying that anti-leukemia immune responses may play a role in leukemia treatment.
Professor Nicolai Reshetikhin
University of California, Berkeley
Understanding Random Surfaces
Monday, December 20, 2010, 4:30pm
Ungar Room 402
Abstract: There is a bijection between a class of piece-wise linear surfaces and dimer configurations on planar graphs. A dimer configuration on a graph is a perfect matching on vertices connected by edges. Dimers are well known in biology, chemistry and statistical mechanics. For certain very natural probability measures on dimer configurations, important correlation functions can be computed as Pfaffians of N\times N matrices. This reduces the statistics of such special random surfaces to a reasonable problem in linear algebra. This allows to study such random surfaces corresponding tolarge graphs. The talk will outline this story and at the end the discussion will focus on the "continuum limit" of such random surfaces.
Professor Pierre Magal
University of Bordeaux, France
Bifurcation Problems for Structured Population Dynamics Models
Monday, December 6, 2010, 4:30pm
Ungar Room 402
Abstract: This presentation is devoted to bifurcation problems for some classes of PDE arising in the context of population dynamics. The main difficulty in such a context is to understand the dynamical properties of a PDE with non-linear and non-local boundary conditions. A typical class of examples is the so called age structured models. Age structured models have been well understood in terms of existence, uniqueness, and stability of equilibria since the 80's. Nevertheless, up to recently, the bifurcation properties of the semiflow generated by such a system has been only poorly understood.
In this presentation, we will start with some results about existence and smoothness of the center mainfold, and we will present some general Hopf bifurcation results applying to age structured models. Then we will turn to normal theory in such a context. The point here is to obtain formula to compute the first order terms of the Taylor expansion of the reduced system.
Dr. Steven White
Centre for Ecology & Hydrology
Wallingford, Oxon, UK
Controlling Mosquitoes by Classical or Transgenic Sterile Insect Techniques
Monday, November 22, 2010, 4:00pm
Ungar Room 402
Abstract: For centuries, humans have attempted to control insect populations. This is in part because of the significant mortality and morbidity burden associated with insect vector-borne diseases, but also due to the huge economic impact of insect pests leading to losses in global food production. The development of transgenic technologies, coupled with sterile insect techniques (SIT), is being explored in relation to new approaches for the biological control of insect pests.
In this talk, I explore the impact of two control strategies (classical SIT and transgenic late-acting bisex lethality) using a stage-structured mathematical model, which is parameterized for the mosquito Aedes aegypti, which can spread yellow fever, dengue fever and Chikungunya disease. Counter to the majority of studies, I use realistic pulsed release strategies and incorporate a fitness cost, which is manifested as a reduction in male mating competitiveness.
I will explore the timing of control release in constant and cyclic wild-type mosquito populations, and demonstrate that this timing is critical for effective pest management. Furthermore, I will incorporate these control strategies into an integrated pest management program (IPM) and find the optimal release strategy. Finally, I will extend the models to a spatial context, determining conditions for the prevention of mosquito invasion by the use of a barrier wall.
Dr. Kate Petersen
Florida State University
The Euclidean Algorithm and Primitive Roots
Thursday, November 18, 2010, 5:00pm
Ungar Room 402
Abstract: Artin's famous primitive root conjecture states that if n is an integer other than -1 or a square, then there are infinitely many primes p such that n is a primitive root modulo p. Although this conjecture is not known to hold for any value of n, Hooley proved it to be true under the assumption of the generalized Riemann hypothesis (GRH). We will discuss a number field version of this conjecture and its connection to the following Euclidean algorithm problem. Let O be the ring of integers of a number field K. It is well-known that if O is a Euclidean domain, then O is a unique factorization domain. With the exception of the imaginary quadratic number fields, it is conjectured that the reverse implication is true. This was proven by Weinberger under the assumption of the GRH. We will discuss recent progress towards the unconditional resolution of the Euclidean algorithm problem and the related primitive root problem. This is joint work with M. Ram Murty.
Dr. Shiwang Ma
Nankai University, China
Bounded and Unbounded Motions for Asymmetric Oscillators at Resonance
Monday, November 8, 2010, 4:30pm
Ungar Room 402
Abstract: In this talk, we consider the boundedness and unboundedness of solutions for the asymmetric oscillator
x" + ax + - bx - + g(x) = p(t) ,
where x + = max{ x,0}, x - = max{- x,0}, a and b are two positive constants, p(t) is a 2π-periodic smooth function and g(x) satisfies lim |x|→+∞x -1g(x) = 0. We establish some sharp sufficient conditions concerning the boundedness of all the solutions and the existence of unbounded solutions. Unlike many existing results in the literature where the function g(x) is required to be a bounded function with asymptotic limits, here we allow g(x) be unbounded or oscillatory without asymptotic limits. Some critical cases will also be considered.
Dr. Igor Rodnianski
Princeton University
Evolution Problem in General Relativity
Wednesday, November 3, 2010, 5:00pm
Ungar Room 402
Abstract: The talk will introduce basic mathematical concepts of General Relativity and review the progress, main challenges and open problems, viewed through the prism of the evolution problem. I will illustrate interaction of Geometry and PDE methods in the context of General Relativity on examples ranging from incompleteness theorems and formation of trapped surfaces to stability problems.
Dr. Lars Andersson
Albert Einstein Institute
The Black Hole Stability Problem
Friday, October 22, 2010, 4:00pm
Ungar Room 402
Abstract: The problem of nonlinear stability for the Kerr model of a rotating black hole is one of the central problems in general relativity. The analysis of linear fields on the Kerr spacetime is an important model problem for full nonlinear stability. In this talk, I will present recent work with Pieter Blue which makes use of the hidden symmetry related to the Carter constant to circumvent these difficulties and give a "physical space" approach to estimates for the wave equation, including energy bounds, trapping, and dispersive estimates. I will also discuss the field equations for higher spin fields including linearized gravity.
Dr. Yuan Lou
Ohio State University
Persistence of a Single Phytoplankton Species
Thursday, October 21, 2010, 4:30pm
Ungar Room 402
Abstract: Phytoplankton need light to grow. However, most of phytoplankton are heavier than water, so they sink. How can phytoplankton persist? We investigate a nonlocal reaction-diffusion-advection equation which models the growth of a single phytoplankton species in a water column where the species depends solely on light for its metabolism. We study the effect of sinking rate, water column depth and vertical turbulent diffusion rate on the persistence of a single phytoplankton species. This is based upon a joint work with Sze-Bi Hsu, National Tsing-Hua University.
Professor Nick Loehr
Virginia Tech
Macdonald Polynomials in Representation Theory and Combinatorics
Friday, October 8, 2010, 4:30pm
Ungar Room 402
Abstract: This talk surveys some recent work in algebraic combinatorics that illustrates surprising connections between representation theory and enumerative combinatorics. We describe how to calculate the Hilbert series of various spaces of polynomials (harmonics, diagonal harmonics, and Garsia-Haiman modules) using combinatorial statistics on permutations and parking functions. This leads to a discussion of the algebraic and combinatorial significance of the Macdonald polynomials, which have played a central role in the theory of symmetric functions for the past two decades.
Brian J. Coburn, Ph.D.
Center for Biomedical Modeling
Semel Institute of Neuroscience and Human Behavior
David Geffen School of Medicine
University of California, Los Angeles
Modeling Approaches for Influenza and HIV
Wednesday, September 8, 2010, 4:00pm
Ungar Room 402
Abstract: In this talk, I will present a survey of research projects on different mathematical models for influenza and HIV. For influenza, I will discuss two different modeling approaches. In the first approach, I will present a multi-strain/multi-host (MSMH) model that tracks the spread of inter-species strains between birds, pigs and humans. In the MSMH model, pigs are "mixing vessels" between avian and human strains and are capable of producing super-strains as a consequence of genetic recombination of these strains. I will show how specific subtypes can cause an epidemic then virtually disappear for years or even decades before reemerging (e.g., the case of H1N1). In the second approach, I will present a model that tracks the spread of influenza within flight transmission. A plane flight is much shorter scale than influenza's infectious duration; hence, we use methods from microbial risk management to assess the number of potential infections. We show that the flight duration along with the compartment will ultimately determine the passenger's risk. For HIV, I will present cross-sectional data on HIV prevalence in Lesotho, a small sub-Saharan African nation with HIV prevalence at approximately 23%. I will present our current progress on data analysis from the Health and Demographic Survey (DHS) to develop risk maps by district based on prevalence and treatment, feasibility analysis of a clinical trial, and efficacy of male circumcision as prevention for HIV.
Dr. Andrew Noble
University of Maryland
A Non-neutral Theory of Dispersal-limited Community Dynamics
Thursday, April 22, 2010, 4:30pm
Ungar Room 402
Abstract: We introduce the first analytical model of a dispersal-limited, niche-structured community to yield Hubbell's neutral theory in the limit of functional equivalence among all species. Dynamics of the multivariate species abundance distribution (SAD) for an asymmetric local community are modeled explicitly as a dispersal-limited sampling of the surrounding metacommunity. Coexistence may arise either from approximate functional equivalence or a competition-colonization tradeoff. At equilibrium, these symmetric and asymmetric mechanisms both generate unimodal SADs. Multiple modes only arise in asymmetric communities and provide a strong indication of non-neutral dynamics. Although these stationary distributions must be calculated numerically in the general theory, we derive the first analytical sampling distribution for a nearly neutral community where symmetry is broken by a single species distinct in ecological fitness and dispersal ability. Novel asymptotic expansions of hypergeometric functions are developed to make evaluations of the sampling distribution tractable for large communities. In this regime, population fluctuations become negligible. A calculation of the macroscopic limits for the symmetric and asymmetric theories yields a new class of deterministic competition models for communities of fixed-size where rescue effects facilitate coexistence. For nearly neutral communities where the asymmetric species experiences linear density-dependence in ecological fitness, strong Allee-type effects emerge from a saddle-node bifurcation at a critical point in dispersal limitation. The bistable dynamics governing a canonical Allee effect are modified by a constant influx of migrants, which raises the lower stable fixed point above zero. In the stochastic theory, a saddle-node bifurcation corresponds to the development of bimodal stationary distributions and the emergence of inflection points in plots of mean first-time to extirpation as a function of abundance.
Dr. Hao Wang
University of Alberta
The Role of Light and Nutrients in Aquatic Trophic Interactions
Friday, April 16, 2010, 4:30pm
Ungar Room 402
Abstract: Carbon (C), nitrogen (N), and phosphorus (P) are vital constituents in biomass: C supplies energy to cells, N is essential to build proteins, and P is an essential component of nucleic acids. The scarcity of any of these elements can severely restrict organism and population growth. Thus in nutrient deficient environments, the consideration of nutrient cycling, or stoichiometry, may be essential for population models. To show this idea, I will present two case studies in this talk.
We carried out a microcosm experiment evaluating competition of an invasive species Daphnia lumholtzi with a widespread native species, Daphnia pulex. We applied two light treatments to these two different microcosms and found strong context-dependent competitive exclusion in both treatments. To better understand these results we developed and tested a mechanistically formulated stoichiometric model. This model exhibits chaotic coexistence of the competing species of Daphnia. The rich dynamics of this model as well as the experiment allow us to suggest some plausible strategies to control the invasive species D. lumholtzi.
We modeled bacteria-algae interactions in the epilimnion with the explicit consideration of carbon (energy) and phosphorus (nutrient). We hypothesized that there are three dynamical scenarios determined by the basic reproductive numbers of bacteria and algae. Effects of key environmental conditions were examined through these scenarios. Competition of bacterial strains were modeled to examine Nishimura's hypothesis that in severely P-limited environments such as Lake Biwa, P-limitation exerts more severe constraints on the growth of bacterial groups with higher nucleic acid contents, which allows low nucleic acid bacteria to be competitive.
Dr. Sanja Zivanovic
Centrum Wiskunde en Informatica (CWI), Amsterdam, Netherlands
Numerical Solutions to Noisy Systems
Thursday, April 15, 2010, 5:00pm
Ungar Room 402
Abstract: We study input-affine systems where input represents some bounded noise. The system can be rewritten as differential inclusion describing the evolution. Differential inclusions are a generalization of differential equations with multivalued right-hand side. They have applications in many areas of science, such as mechanics, electrical engineering, the theory of automatic control, economical, biological, and social macrosystems. A numerical method for rigorous over-approximation of a solution set of input-affine system will be presented. The method gives high order error for a single time step and a uniform bound on the error over the finite time interval. The approach is based on the approximations of inputs by piecewise linear functions.
Dr. Priyanga Amarasekare
University of California Los Angeles
Ecological and Evolutionary Consequences of Dispersal in Multi-trophic Communities
Friday, March 12, 2010, 4:30pm
Ungar Room 402
Abstract: I investigate the effects of non-random dispersal strategies on coexistence and species distributions in multi-trophic communities with competition and predation. I conduct a comparative analysis of dispersal strategies with random and fitness-dependent dispersal at the extremes and two intermediate strategies that rely on cues (density and habitat quality) that serve as proxies for fitness. The most important finding is an asymmetry between consumer species in their dispersal effects. The dispersal strategy of inferior resource competitors that are less susceptible to predation have a large effect on both coexistence and species distributions, but the dispersal strategy of the superior resource competitor that is more susceptible to predation has little or no effect on dispersal. I explore the consequences of this asymmetry for the evolution of dispersal.
Dr. Herbert Wilf
Thomas A. Scott Emeritus Professor of Mathematics
University of Pennsylvania
How to Lose as Little as Possible
Thursday, March 11, 2010, 5:00pm
Ungar Room 402
Abstract: Suppose Alice has a coin with heads probability q and Bob has one with heads probability p > q. Now each of them will toss their coin n times, and Alice will win iff she gets more heads than Bob does. Of course, the game favors Bob, but for the given p, q, what is the choice, N(q,p), of n that maximizes Alice's chances of winning? The analysis uses the multivariate form of Zeilberger's algorithm, so a portion of the talk will be a review of the ideas underlying symbolic summation.
Dr. Mario Milman
Florida Atlantic University
Sobolev Inequalities on Probability Metric Spaces
Friday, March 5, 2010, 5:00pm
Ungar Room 402
Abstract: To formulate new Sobolev inequalities one needsto answer questions like: what is the role of dimension? What norms are appropriate to measure the integrabilitygains? Just to name a few...For example, in contrast to the Euclidean case, the integrability gains in Gaussian measure are logarithmic but dimension free (log Sobolev inequalities). So it is easy to understand the difficulties to derive a general theory. I will discuss some new methods to prove general Sobolev inequalities that unify the Euclidean and the Gaussian cases, as well as several important model manifolds.
CANCELLED
Dr. Larry Shepp
Rutgers University
Member, National Academy of Science (NAS)
Member, Institute of Medicine (IOM)
Problems in Probability
Friday, February 26, 2010, 5:00pm
Ungar Room 402
Abstract: Several problems will be discussed: 1) What is the distribution of the empirical correlation coefficient of two (actually independent) Wiener processes? It is far from zero - correlation is induced by the arc sine law property of the sample paths. This is used by (bad) statisticians to show correlation between time series when none exists. It is a non-trivial calculation to find the actual distribution. 2) What is the relationship between the coefficients of a polynomial of degree n and the number of its real zeros? Descartes had something to say about it, but Mark Kac showed that probability theory can add a lot of insight. 3) An update on the situation discussed last year re the artificial pancreas project.
Dr. Richard Schoen
Bass Professor of Humanities and Sciences
Stanford University
Riemannian Manifolds of Constant Scalar Curvature
Tuesday, February 23, 2010, 5:00pm
Ungar Room 402
Abstract: The problem of constructing Riemannian metrics of constant scalar curvature is called the Yamabe problem. It is an important variational problem in conformal geometry, and also relates directly to the Einstein equations of general relativity. We will give a brief history and introduction to this problem and describe some new phenomena which have been discovered recently concerning issues of singular behavior and blow up of such metrics.
Dr. Pengzi Miao
School of Mathematical Sciences
Monash University
Critical Metrics for the Volume Functional on Compact Manifolds with Boundary
Thursday, February 4, 2010, 5:00pm
Ungar Room 402
Abstract: It is known that, on closed manifolds, Einstein metrics of negative scalar curvature are critical points of the usual volume functional constrained to the space of metrics of constant scalar curvature. In this talk, I will discuss how this variational characterization of Einstein metrics can be localized to compact manifolds with boundary. I will derive the critical point equation and focus on geometric properties of its solutions. In particular, if a solution has zero scalar curvature and the boundary of the manifold can be isometrically embedded into the Euclidean space as a convex hypersurface, I will show that the volume of such a critical metric is always greater than or equal to the Euclidean volume enclosed by the image of the isometric embedding, and two volumes are the same if and only if the critical metric is isometric to the Euclidean metric on a round ball. I will also give a classification of all conformally flat critical metrics. This is joint work with Luen-Fai Tam.
Dr. Brian J. Weber
RTG/Simons Center Postdoc
Stony Brook University
Einstein Metrics, the Bach Tensor, and Metric Degenerations
Monday, February 1, 2010, 5:00pm
Ungar Room 402
Abstract: One might search for "canonical metrics," such as Einstein metrics, on a manifold by trying to prove the convergence of a sequence of metrics that minimize some functional, although such a direct approach usually fails. In this talk we present an indirect approach which has been successful in some cases. A local obstruction to finding an Einstein metric in a conformal class is the non-vanishing of the Bach tensor, defined to be the gradient of the Weyl curvature functional $\int |W|^2$. On a Kaehler manifold there are no other obstructions, and any Bach-flat Kaehler metric is locally conformally Einsteinian. Additionally, the conformal factor is geometrically interesting and sometimes controllable. This talk will describe the results of a 2008 paper with X. Chen and C. LeBrun, where circumstances under which a Kaehler manifold is Bach-flat were established, and where it was shown that these conditions hold for a certain Kaehler metric on $CP^2 # 2\overline CP^2$ with non-zero conformal factor, establishing for the first time an Einstein metric on $CP^2 # 2\overline 2CP^2$.
Dr. Hans Boden
McMaster University
Metabelian SL(n,C) Representations of Knot Groups
Thursday, January 28, 2010, 5:00pm
Ungar Room 402
Abstract: In this talk, which represents joint work with Stefan Friedl, we will present a classification of irreducible metabelian SL(n,C) representations of knots groups. Under a mild hypothesis, we prove that such representations factor through a finite group, hence they are all conjugate to unitary representations, and we give a simple formula for the number of conjugacy classes. For knots with nontrivial Alexander polynomial, we discuss an existence result for irreducible metabelian representations. Given a knot group, its SL(n,C) character variety admits a natural action by the cyclic group of order n, and we show how to identify the fixed points of this action with characters of metabelian representations. If time permits, we will describe conditions under which such points are simple points in the character variety using a deformation argument of Abdelghani, Heusener, and Jebali.
Dr. Brett L. Kotschwar
C.L.E. Moore Instructor
Massachusetts Institute of Technology
Backwards Uniqueness for the Ricci Flow and the Non-expansion of the Isometry Group
Monday, January 25, 2010, 5:00pm
Ungar Room 402
Abstract: One of the fundamental properties of the Ricci flow -- an evolution equation for Riemannian metrics -- is that of isometry preservation, namely, that an isometry of the initial metric remains an isometry of the solution, at least as long as the curvature remains bounded. In this talk, I will take up the complementary problem of isometry development under the flow. While the solution may acquire new isometries in the limit, one does not expect the flow to sponsor their generation within the lifetime of the solution. The impossibility of such a phenomenon is equivalent to a backwards uniqueness (or unique-continuation) property for the equation: two solutions which agree at some non-initial time must agree identically at all previous times. I will discuss recent work which establishes this property for complete solutions of bounded curvature, and prohibits, additionally, a solution from becoming Einstein or self-similar in finite time.
Dr. Stephen Gourley
University of Surrey, UK
Impulsive Delay Equation Models for the Control of Vector-borne Diseases
Friday, January 15, 2010, 4:00pm
Ungar Room 402
Abstract: Delay equation models for the control of a vector-borne disease such as West Nile virus will be presented. The models make it possible to compare the effectiveness of larvicides and adulticides in controlling mosquito populations. The models take the form of autonomous delay differential equations with impulses (if the adult insects are culled) or a system of nonautonomous delay differential equations where the time-varying coefficients are determined by the culling times and rates (in the case where the insect larvae are culled). Sufficient conditions can be derived which ensure eradication of the disease. Eradication of vector-borne diseases is possible by culling the vector at either the immature or the mature phase. Very infrequent culling can actually lead to the mean insect population being increased rather than decreased.
Professor Philippe LeFloch
University of Paris 6 and CNRS
Einstein Spacetimes with Bounded Curvature
Thursday, December 10, 2009, 4:30pm
Ungar Room 402
Abstract: I will present recent results on Einstein spacetimes of general relativity when the curvature is solely assumed to be bounded and no assumption on its derivatives is made. One such result, in a joint work with B.-L. Chen, concerns the optimal regularity of pointed spacetimes in which, by definition, an "observer" has been specified. Under geometric bounds on the curvature and injectivity radius near the observer, there exist a CMC (constant mean curvature) foliation as well as CMC--harmonic coordinates, which are defined in geodesic balls with definite size depending only on the assumed bounds, so that the components of the Lorentzian metric has optimal regularity in these coordinates. The proof combines geometric estimates (Jacobi field, comparison theorems) and quantitative estimates for nonlinear elliptic equations with low regularity.
CANCELLED
Dr. Zhilan Feng
Purdue University
Evolutionary Implications of Influenza Medication Strategies
Tuesday, November 24, 2009, 5:00pm
Ungar Room 402
Abstract: Patients at risk for complications of influenza are commonly treated with antiviral medications, which however also could be used to control outbreaks. The adamantanes and neuraminidase inhibitors are active against influenza A, but avian influenza (H5N1) is resistant to oseltamivir and swine influenza (H1N1) to the adamantanes (but see postscript). To explore influenza medication strategies (pre-exposure or prophylaxis, post-exposure/pre-symptom onset, and treatment at successive clinical stages) that may affect evolution of resistance (select for resistant strains within or facilitate their spread between hosts), we elaborated a published transmission model and chose parameters from the literature. Then we derived the reproduction numbers of sensitive and resistant strains, peak and final sizes, and time to peak. Finally, we made these results accessible via user-friendly Mathematica notebooks. (Joint work with Rongsong Liu, Dashun Xu, Yiding Yang, and John Glasser)
Professor Sergiy Koshkin
University of Houston-Downtown
Gauge Theory of Faddeev-Skyrme Functionals
Friday, November 20, 2009, 3:30pm
Ungar Room 402
Abstract: We study geometric variational problems for a class of nonlinear sigma-models in quantum field theory. Mathematically, one needs to minimize an energy functional on homotopy classes of maps from closed 3-manifolds into compact homogeneous spaces G/H, similar to the case of harmonic maps. The minimizers are known as Hopfions and exhibit localized knot-like structure. Our main results include proving existence of Hopfions as finite energy Sobolev maps in each (generalized) homotopy class when the target space is a symmetric space. For more general spaces we obtain a weaker result on existence of minimizers in each 2-homotopy class.
Our approach is based on representing maps into G/H by equivalence classes of flat connections. The equivalence is given by gauge symmetry on pullbacks of G-->G/H bundles. We work out a gauge calculus for connections under this symmetry, and use it to eliminate non-compactness from the minimization problem by fixing the gauge.
Dr. Alexander Engström
Miller Research Fellow
University of California, Berkeley
Graph Theoretic Methods in Algebraic Statistics
Thursday, November 12, 2009, 5:00pm
Ungar Room 402
Abstract: First I will review how methods from commutative algebra, for example Gröbner bases and toric ideals, can be used in statistics. Then I will describe two applications of graph theoretic methods in this context: My proof of Sturmfels and Sullivant's conjecture on cut ideals; and the ideals of graph homomorphisms introduced together with Patrik Noren.
Dr. Daniel Ruberman
Brandeis University
Slice Knots and the Alexander Polynomial
Thursday, November 5, 2009, 5:00pm
Ungar Room 402
Abstract: A knot in the 3-sphere is slice if it bounds an embedded disk in the 4-ball. The disk may be topologically embedded, or we may require the stronger condition that it be smoothly embedded; the knot is said to be (respectively) topologically or smoothly slice. It has been known since the early 1980's that there are knots that are topologically slice, but not smoothly slice. These result from Freedman's proof that knots with trivial Alexander polynomial are topologically slice, combined with gauge-theory techniques originating with Donaldson. In joint work with C. Livingston and M. Hedden, we answer the natural question of whether Freedman's result is responsible for all topologically slice knots. We show that the group of topologically slice knots, modulo those with trivial Alexander polynomial, is infinitely generated. The proof uses Heegaard-Floer theory.