Symposium on Algebraic and Geometric Combinatorics - Abstracts

Abstract: The concepts of "nonnesting" and "noncrossing" partitions extend in a beautiful way to any finite Weyl group W. Both sets of objects are counted by the Catalan number Cat(W). However: while there exist uniform proofs that |NN(W)|=Cat(W), the only known proof that |NC(W)|=Cat(W) is case-by-case, using computer in the exceptional types. This is a serious flaw in our understanding. In this talk I will present the first uniform bijection between NN(W) and NC(W). Unfortunately, our proof that the bijection exists is currently case-by-case (hence we STILL don't know why |NC(W)|=Cat(W)). Fortunately, the proof involves new and interesting combinatorics, even in type A. Along the way we can prove some conjectures of Panyushev, and of Bessis and Reiner.

This is joint work with Christian Stump and Hugh Thomas.

Abstract: We discuss the enumeration theory for flags in Eulerian partially ordered sets, emphasizing the two main geometric and algebraic examples, face posets of convex polytopes and regular CW-spheres, and Bruhat intervals in Coxeter groups. We review the two algebraic approaches to flag enumeration - one essentially as a quotient of the algebra of noncommutative symmetric functions and the other as a subalgebra of the algebra of quasisymmetric functions - and their relation via duality of Hopf algebras. One result is a direct expression for the Kazhdan-Lusztig polynomial of a Bruhat interval in terms of a new invariant, the complete cd-index. Finally, we summarize the theory of combinatorial Hopf algebras, which gives a unifying framework for the quasisymmetric generating functions developed here.

Abstract: The FKG inequality of Fortuin, Kasteleyn and Ginibre (1971) originated as a correlation inequality in statistical mechanics. It has many applications in discrete probability and extremal combinatorics.

In this talk, after reviewing some of the background, we present a polynomial coefficient-wise inequality that refines the original FKG inequality. This polynomial FKG inequality has applications to f-vectors of joins of simplicial complexes, to Betti numbers of intersection of Schubert varieties, and to power series weighted by Young tableaux. The latter case includes a correlation-type inequality for Plancherel measure on integer partitions, and for its poissonization.

The talk will mostly be quite elementary and no previous familiarity with these topics will be assumed.

Abstract: A few years ago, Dennis Stanton asked for a topological explanation for the fact that the Gaussian polynomial evaluated at -1 yields the number of self-complementary partitions in a rectangle, and for related instances of Stembridge's q=-1 phenomenon. In joint work with John Shareshian and Dennis Stanton, we provide such an explanation by introducing chain complexes whose "face numbers" are the coefficients in the Gaussian polynomial and whose homology is concentrated in even dimensions. These complexes make sense in more generality, but do not always have such homology concentration. I will discuss a short, topological proof that these complexes are acyclic whenever they are odd dimensional as well as a related chain complex whose "face numbers" count partitions in a 3-dimensional box and whose homology is again concentrated in dimensions all of the same parity, with homology basis indexed by semistandard domino tableaux of rectangular shape.

Abstract: We will discuss tilings of regions of the plane using prescribed pieces (tiles). A familiar non-mathematical example is a jigsaw puzzle. We will consider such questions as the following. Is there a tiling? If so, how many? If we can't say exactly how many tilings there are, is there a good approximation? Is a tiling easy to find? Is it easy to convince someone that a tiling doesn't exist? What does a "typical" tiling look like? How are different tilings related? These questions involve interesting aspects of combinatorics, computer science, logic, algebra, geometry and analysis.

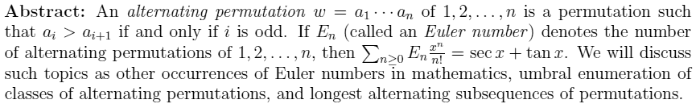
For further information contact Michelle Wachs wachs@math.miami.edu