Some derived theorems from BCT such as uniform boundedness theorem and open mapping theorem and in particular their applications are also introduced.
Chris Anderson
University of Miami
will present
An Introduction to the Alexander Invariant and Alexander Polynomial
Friday, February 3, 2017, 4:00pm
Ungar Building Room 402
Abstract: In this talk I will offer a brief introduction to the Alexander invariant as well as the related Alexander polynomial of a knot and the multivariable Alexander Polynomial of a link. In particular, examples illustrating methods of calculating these invariants will be presented. We will also discuss some information carried by these invariants, with special focus on knots and links with trivial Alexander polynomial.
Jorge Cardona
University of Miami
will present
Multiplication of Distributions
Friday, November 11, 2016, 5:00pm
Ungar Building Room 402
Abstract: In this talk we will review few examples where the notion of multiplication of distributions is needed, together with L. Schwartz's (1954) counterexample in the impossibility of a "natural" theory of such product. We will consider two ways to solve this issue: using L. Hörmander (1970) construction based on wave front sets and the theory of J.F. Colombeau (1984), the now called Colombeau algebra of "new" generalized functions, if time allows some basic examples in PDE will be revisited.
James McKeown
University of Miami
will present
An Introduction to Hyperplane Arrangements
Friday, November 4, 2016, 5:00pm
Ungar Building Room 402
Abstract: A hyperplane is an n-1 dimensional subspace of an n dimensional vector space. When the vector space is R^n, the complement of the hyperplanes is a collection of polyhedral regions. It is natural to ask how many of these polyhedral regions there are, and how many of them are bounded. This turns out to be a purely combinatorial problem and has a nice answer in terms of the Characteristic Polynomial of the arrangement. We will define this polynomial, and see that it generalizes the classical chromatic polynomial of a graph. Time permitting, we will introduce "the finite field method" as a computational tool for finding characteristic polynomials of arrangements.
Moses Koppendrayer
University of Miami
will present
Quasipositivity and the Ozsvath and Szabo Contact Invariant
Friday, October 28, 2016, 5:00pm
Ungar Building Room 402
Abstract: Matthew Hedden proved that a fibered knot being strongly quasipositive is equivalent to the Ozsvath and Szabo contact invariant associated to it being non-zero. I will give background to understand this theorem, as well as give insight into avenues of future research.
August Hozie
University of Miami
will present
The Arithmetization of Syntax
Friday, October 14, 2016, 5:00pm
Ungar Building Room 402
Abstract: Through a technique referred to as the arithmetization of syntax, Godel effectively transformed metamathematical statements into statements that could fit inside first order arithmetical systems. In this talk I explore a particular concrete case of Godel’s work, the incompleteness of Peano Arithmetic, and discuss the philosophical and historical significance of the result.
Victor Garcia Herrero
University of Miami
will present
Numerical and geometrical fallacies
Friday, September 30, 2016, 5:00pm
Ungar Building Room 402
Abstract: One of the pedagogical tools that can be used for teaching mathematics are the mathematical fallacies. We often extrapolate properties to objects that don't have the desired property or consider a picture of a geometrical problem as the only possible case. In this talk, we will discuss some numerical and geometrical fallacies and how to use them to teach fundamental concepts in algebra, analysis and geometry.
Chris Langdon
University of Miami
will present
Symmetric Twisted Differentials on Projective Subvarieties
Friday, September 23, 2016, 5:00pm
Ungar Building Room 402
Abstract: It was shown by M. Schneider in the nineties that there are no symmetric differentials of degree m on projective subvarieties of low codimension even if twisted by O(k) for k<m. In this talk we will discuss the geometric nature of the extremal case k=m and its relation to the quadric hypersurfaces containing the subvariety.
Eric Ling
University of Miami
will present
Quantum Theory and the Origin of Spin
Friday, September 16, 2016, 5:00pm
Ungar Building Room 402
Abstract: "No theorist in his right mind would have invented quantum mechanics unless forced to by data" - Craig Hogan. In this talk I will give a brief overview of the (frustrating) origins of quantum mechanics. I will show how we can use the Stern-Gerlach experiment (and its experimental discovery of spin) to determine what the axioms of quantum mechanics ought to be and demonstrate why the underlying space is a Hilbert space. Lastly, I will show how Dirac was able to combine quantum theory and relativity to theoretically predict spin, and while doing so, he inadvertently predicted antimatter.
Brittney Ellzey
University of Miami
will present
Interval Graphs and Circular Arc Graphs
Friday, September 9, 2016, 5:00pm
Ungar Building Room 402
Abstract: Suppose we have a collection of n intervals on the real line. We can create a graph on n vertices by letting each interval correspond to a vertex and drawing an edge between two vertices if their corresponding intervals overlap. These graphs are called interval graphs. We will look at some examples of proper and unit interval graphs, as well as some different ways of characterizing them. We will also look at circular arc graphs, which are a generalization of interval graphs in which the intervals on the real line become arcs around a circle. If time permits, we will discuss some open problems involving the graphs mentioned and their chromatic symmetric/quasisymmetric functions.
Armando Cabrera
University of Miami
will present
Relativity in 1+1 dimensions?
Friday, April 22, 2016, 5:00pm
Ungar Building Room 402
Abstract: A spacetime is a 4-dimensional time-orientable Lorentzian manifold that satisfies the Einstein equations. These equations are formulated in tensorial form and its analysis, for various reasons, is complicated. In mathematics and physics, sometimes one can gain some insight of a problem by considering a low-dimensional analog of it; therefore, it is natural to ask if we can do that with the Einstein equations. The goal of this talk is to review some basic facts about the Einstein equations and to investigate whether it is possible to consider a meaningful (1+1)-dimensional analog of them.
Jorge Cardona
University of Miami
will present
PDEs on Curved Space Time
Friday, April 15, 2016, 5:00pm
Ungar Building Room 402
Abstract: We will review basic aspects on how to numerically solve a few PDEs on flat space-times, starting with the scalar wave equation in 1+1 and 2+1. Then we will use the Schwarzschild metric to see the effect of a curved space on the equation, and lastly we will look at an example of how to find the metric numerically that solves a certain PDE.
Ondrej Zjevik
University of Miami
will present
Numerical Quadrature
Friday, April 8, 2016, 5:00pm
Ungar Building Room 402
Abstract: In modern terminology the term “quadrature” represents the numerical evaluation of a definite integral. It is well documented that Archimedes of Syracuse (287 BC – 212 BC) derived formulas for the surface area and volume of a sphere, and the area under a parabola. In this talk, we will focus on the modern development of numerical integration based on different interpolation methods. We will derive and compare the Newton—Cotes formulas and Gaussian quadrature formulas. Extending these formulas for multidimensional integrals is possible due to the Fubini’s theorem, but the computational complexity grows exponentially. We will discuss two methods that avoid this phenomenon.
Eric Ling
University of Miami
will present
Before the Big Bang?
Friday, April 1, 2016, 5:00pm
Ungar Building Room 402
Abstract: The Friedman-Robertson- Walker (FRW) spacetimes are the standard models of cosmology which accurately describe the universe as a whole. However, they make the striking prediction that the universe began a finite amount of time ago at the big bang. Mathematically, this means that one cannot embed the FRW spacetimes as a proper subset of another spacetime, (M,g), so long as the the metric regularity class of g is at least C^2. Therefore a natural question to ask is if one can extend an FRW spacetime properly into another spacetime, (M,g), with g satisfying a lower regularity class, say C^0? In this talk I will explain the origin of the FRW spacetimes and why they are good models for describing the universe. Then I will show how they predict the big bang and why extensions are impossible if g is at least C^2. Finally, I will show that if one considers 2-dimensional FRW spacetimes (i.e. one time dimension and one space dimension), then a C^0 extension is possible. The question remains open for higher dimensional FRW spacetimes.
Moses Koppendrayer
University of Miami
will present
Prime Knot Theorem
Friday, March 25, 2016, 5:00pm
Ungar Building Room 402
Abstract: In this talk I will discuss the Prime Knot Theorem which states that there are knots that cannot be produced from non-trivial knots under the operation of connected sum. The theorem is pretty simple, but I will use it to demonstrate techniques in Algebraic Topology as I sketch two or three proofs of the theorem.
James McKeown
University of Miami
will present
The Combinatorics of the Waldspurger Decomposition
Friday, February 19, 2016, 5:00pm
Ungar Building Room 402
Abstract: In 2005 J.L. Waldspurger proved a remarkable theorem. Given a finite reflection group G, the closed cone over the positive roots is equal to the disjoint union of images of the open weight cone under the action of 1-g. When G is taken to be the symmetric group the decomposition is related to the familiar combinatorics of permutations but also has some surprising features. To see this, we give a nice combinatorial description of the decomposition.
Michela di Marca
University of Genova
will present
On the diameter of dual graphs of projective varieties
Friday, February 12, 2016, 6:00pm
Ungar Building Room 506
Abstract: The concept of dual graph of a projective variety can be studied both from a geometric and from an algebraic point of view, by considering the homogeneous ideal associated to the variety in a certain polynomial ring. I will focus on the second aspect and I will investigate some restrictions on the diameter of such graphs when we start from a coordinate ring with good properties. In particular, I will show an upper bound for the diameter based on the distribution of degrees on the irreducible components of the variety.
Andy Smith
University of Miami
will present
An Introduction to the Surreal Numbers
Friday, February 5, 2016, 5:00pm
Ungar Building Room 402
Abstract: The surreal numbers form an ordered field, and, informally speaking, contain every other ordered field as subfields. During this talk, we will first revisit some familiar fields and the properties that they satisfy. Once we establish an understanding of these fundamental fields, we will explore motivations for the construction of the surreal numbers, followed by a verification that these new “numbers” indeed form an ordered field. We will then apply this newfound understanding of the surreal numbers as a tool to investigate mathematical games. The lecture will conclude with a discussion of the current research on surreal numbers, namely analysis and integration.
Alexander Lazar
University of Miami
will present
Matroids and the Greedy Algorithm
Friday, January 29, 2016, 5:00pm
Ungar Building Room 402
Abstract: Matroids are combinatorial objects that generalize notions of independence and dimension from combinatorics, linear algebra, and geometry. In this talk, we will present several equivalent definitions of Matroids, and in particular a definition that relates Matroids to problems for which the Greedy Algorithm provides a solution. We will also, if time permits, introduce the Tutte Polynomial, a matroid invariant that generalizes the chromatic polynomial from graph theory.
Yishu Song
University of Miami
will present
A Brief Survey on Quasi-stationary Distribution
Friday, December 4, 2015, 5:00pm
Ungar Building Room 402
Abstract: In this talk, we'll first go over some general properties of quasi-stationary distribution, a probability notion that arises naturally from a variety of natural phenomena. Then, as examples, we'll discuss the quasi-stationary distributions for Birth-Death Process and Feller diffusion and see how the first eigenfunction of a differential equation can explicitly identify the quasi-stationary distribution for the Feller diffusion. This talk is mainly based on the survey paper by Sylvie Meleard and Denis Villemonais.
Jorge Cardona
University of Miami
will present
Hamiltonian Dynamics and PDEs
Friday, November 13, 2015, 5:00pm
Ungar Building Room 402
Abstract: Abstract: In this talk we will discuss some classical aspects of Hamiltonian dynamics on finite dimensional spaces as invariant measures, Liouville's theorem and the Poincare recurrence theorem. We will consider the linear Schrödinger equation, as an infinite dimensional dynamical system, to see how the previous ideas can be applied in that case. If time allows we will discuss some non-linear cases too.
Michael Weiss
University of Miami
will present
Fast Multiplication Algorithms
Friday, November 6, 2015, 5:00pm
Ungar Building Room 402
Abstract: Fast algorithms for multiplication of integers and polynomials are of great importance for calculations in number theory and cryptography where precise results for arbitrarily large numbers is required. In this talk I will give an overview of some of these algorithms that improve upon naive “schoolbook” multiplication (O(n^2)). In particular, I will present Karatsuba’s algorithm and the more general Toom-Cook multiplication algorithms as a class of algorithms that use polynomial interpolation to compute integer and polynomial products. I’ll then describe how they can be constructed as a series of linear transformations and can transformed via the Transposition Principle to algorithms that compute an important, smaller product called the middle product. This talk will focus on understanding the philosophy and general ideas behind the algorithms, and will be lighter on technical considerations such as the specifics of implementation, so coding knowledge or prior familiarity with the subject won’t be required!
Chris Langdon
University of Miami
will present
Groebner Bases
Friday, October 30, 2015, 5:00pm
Ungar Building Room 402
Abstract: Given an ideal I in k[x1,...xn] and a fixed monomial ordering, there exists a special generating set called a Groebner basis. We will look at the construction of these bases and see what information they encode about the affine algebraic variety defined by I. We will see that one of these bases gives the dimension of the variety while another gives information about the projections of the variety onto subspaces of k^n.
Armando Cabrera
University of Miami
will present
Mathematics and General Relativity
Friday, October 23, 2015, 5:00pm
Ungar Building Room 402
Abstract: One hundred years ago, Albert Einstein developed a novel theory, which describes the relation between the matter present in the universe and its geometry. In this talk we will give a gentle introduction to mathematical relativity, from basic definitions to some results about the topology and geometry of black holes.
Brittney Ellzey
University of Miami
will present
An Introduction to Umbral Calculus
Friday, October 16, 2015, 5:00pm
Ungar Building Room 402
Abstract: Umbral calculus is a proof technique in which the indices of sequences of polynomials are treated as exponents. This technique allows us to manipulate these polynomials in a manner that seems “shady.” In this talk, we will see why this method actually works. We will also look at some well-known examples of these sequences of polynomials, such as the Touchard polynomials, Bernoulli polynomials, and Hermite polynomials.
Christopher Anderson
University of Miami
will present
Arrow's Impossibility Theorem
Friday, October 2, 2015, 5:00pm
Ungar Building Room 402
Abstract: In this talk, we will offer a proof of Arrow's impossibility theorem, which states that there is no rank order voting system that satisfies certain "fairness" criteria. While Arrow's theorem is popularly interpreted as "there is no perfect voting system," we will also address the limitations of this interpretation of the theorem. We will also see how various common voting systems violate Arrow's theorem.
Alexander Lazar
University of Miami
will present
Game Theory and Nash Equilibria
Friday, September 25, 2015, 5:00pm
Ungar Building Room 402
Abstract: In this talk, we will give a brief overview of the notion of a Nash Equilibrium from game theory. Using a fixed-point theorem from topology, one can show that a Nash Equilibrium exists for every finite game with perfect information. We will also discuss some of the limitations of the definition of a Nash equilibrium in terms of the theory of extensive games.
Eric Ling
University of Miami
will present
Does the Universe Have a Beginning?
Friday, September 11, 2015, 5:00pm
Ungar Building Room 402
Abstract: Does the universe have a beginning? The big bang theory predicts that it does and it happened 13.7 billion years ago. In this talk I will discuss the motivation for the big bang theory and its limitations to describing the universe. If the big bang theory isn't 100% accurate, then perhaps its prediction that the universe has a beginning is false. Although this question is still debated even today, a couple of theorems by Stephen Hawking and Roger Penrose show that in "physically reasonable" universes, there must be some sort of beginning. I will discuss the implications of these theorems and how they (only almost) answer the question of whether the universe had a beginning.
Drew Armstrong
University of Miami
will present
Mathematics of music
Friday, April 24, 2015, 3:30pm
Ungar Building Room 402
Abstract: Yesterday I finished teaching a course on the mathematics of music. In this talk I will present some of the highlights. The mathematics of music comes in two basic flavors (1) Fourier analysis tells us that most instruments make sounds with harmonics at integer multiples of the fundamental frequency. This together with some psychoacoustics implies that small whole number frequency ratios "sound good". (2) Then, to build a music theory on small whole number ratios means we must come up with good approximate solutions to impossible problems in number theory. The first and most important such approximation is that log(3)/log(2) is very close to 19/12. This is why we divide the octave into 12 tones.
Jorge Cardona
University of Miami
will present
On Schrodinger Equation
Friday, April 17, 2015, 3:30pm
Ungar Building Room 402
Abstract: We will talk about the derivation of the Schrodinger equation, time dependent and independent, using an analogy to classical mechanics based on Feynman's reading of Dirac's work. The concept of observables, common to classical and quantum mechanics, will be described briefly and allow us to derive Heisenberg's uncertainty principle from the relation of the observables of position and momentum. In order to illustrate the subject two examples will be shown: free-particle, and the harmonic oscillator in the classical and quantum case..
Ziqian Ding
University of Miami
will present
Something of Catalan Numbers
Friday, April 10, 2015, 3:30pm
Ungar Building Room 402
Abstract: In combinatorics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems. They first arise in tree enumeration problems of the type: "In how many ways can a regular n-gon be divided into n-2 triangles if different orientations are counted separately? In this talk, we will see some basic properties and give several interpretations of the Catalan numbers. We will also see some bijections between Dyck paths and non-crossing partitions. For the last part, we will step a little further into q-Catalan numbers.
Armando Cabrera
University of Miami
will present
The What, How and Why of Ricci Flow
Friday, April 3, 2015, 3:30pm
Ungar Building Room 402
Abstract: In 1982, Richard Hamilton developed a new powerful technique called ‘Ricci Flow’, which is a beautiful combination of differential geometry and analysis. In some sense, we can think of it as a process to make a space “rounder and rounder”. In this talk, without going into deep details, we will try to gain some intuition of what Ricci flow is and how it works. We will talk about some of its main applications, the most remarkable of which is probably its role in Perelman’s proof of the Poincare conjecture.
Dr. Greg Galloway
University of Miami
will present
On the topology of black holes and beyond
Friday, March 27, 2015, 3:30pm
Ungar Building Room 402
Abstract: In recent years there has been a great deal of interest in black holes in higher dimensional gravity. This, in particular, has led to questions about the topology of black holes in higher dimensions. In this talk we review Hawking's classical theorem on the topology of black holes in 3+1 dimensions (and its connection to black hole uniqueness) and present a generalization of it to higher dimensions. The latter is a geometric result which places restrictions on the topology of black holes in higher dimensions. We shall also discuss recent work on the topology of space exterior to a black hole. This is closely connected to the Principle of Topological Censorship, which roughly asserts that the topology of the region outside of all black holes (and white holes) should be simple. All of the results to be discussed rely on recently developments in the theory of marginally outer trapped surfaces, which are natural spacetime analogues of minimal surfaces in Riemannian geometry. The first part of the talk will be dedicated to a gentle introduction to general relativity and black holes.
Brittney Ellzey
University of Miami
will present
Graph Colorings and Symmetric Functions
Friday, March 20, 2015, 3:30pm
Ungar Building Room 402
Abstract: A proper coloring of a graph is a map that assigns a color to each vertex with the condition that vertices connected by an edge are assigned different colors. Given a nonnegative integer k, the chromatic polynomial counts the number of proper colorings of a graph that use at most k colors. Stanley introduces the chromatic symmetric function of a graph, which generalizes the chromatic polynomial of a graph. Shareshian and Wachs generalize this further to the chromatic quasisymmetric function of a graph. We will look at some examples to get a better idea of what these objects are. We will also look at a few theorems and conjectures about the chromatic symmetric function and their generalizations to the chromatic quasisymmetric function. We will then see how these theorems apply to our examples.
Chris Langdon
University of Miami
will present
The Card Game 'Set' and its structure
Friday, March 6, 2015, 3:30pm
Ungar Building Room 402
Abstract: 'Set' is a card game based on pattern recognition. Interestingly, its rules can be encoded in the linear algebra of a four-dimensional affine space over the finite field with three elements. We will prove a geometric fact about this finite space- the largest a subset can be that avoids all lines is twenty- and use this to conclude a non-trivial fact about the game.
Prayat Poudel
University of Miami
will present
Singular Instanton Knot Homology
Friday, February 20, 2015, 3:30pm
Ungar Building Room 402
Abstract: Singular Instanton Knot homology is an invariant of knots in the 3-sphere. In this talk I will give a motivation for the study of this invariant and give a gentle introduction to how these invariants are computed.
Yishu Song
University of Miami
will present
Diffusion processes and differential equations
Friday, February 13, 2015, 3:30pm
Ungar Building Room 402
Abstract: In this talk, we'll discuss the interaction between diffusion process and differential equations via stochastic calculus. I'll start with basic notions such as martingale, Brownian motion and stochastic differential equations, etc. Then we'll see how classic PDE's are solved via Ito formula. At the end, both as a reason and a consequence of the theory developed, an example of some practical significance will be studied.
Alex Lazar
University of Miami
will present
Set theory and Aronszajn Trees
Friday, February 6, 2015, 3:30pm
Ungar Building Room 402
Abstract: In graph theory,König's Lemma states that any tree with countably many vertices in which every vertex has finite degree must contain an infinite path. The proof of this result is simple, and leads to the natural question of whether analogous results hold for trees with larger sets of vertices. In the 1930s, Aronszajn proved that the analogous result does *not* hold for trees whose vertex set has the cardinality of the continuum by constructing an object that we now call an Aronszajn Tree. In this talk, we will discuss some basic set-theoretic notions such as cardinal and ordinal numbers, and use them to construct an Aronszajn Tree by transfinite induction
David Udumyan
University of Miami
will present
Metric Analysis, properties and applications as a tool for interpolation, approximation and forecasting
Friday, January 30, 2015, 3:30pm
Ungar Building Room 402
Abstract: We will discuss Metric Analysis, a general approach for the study of functional dependencies based on the information of functional values on a finite number of fixed arguments. Effective schemes of interpolation and restoring (smoothing) for functions of one or many variables, as well as forecasting of functional values for functions of one variable, are developed based on Metric Analysis. Applications of these methods and schemes will be given; in particular, their application to restoring energy fields in nuclear reactors.
Ziqian Ding
University of Miami
will present
Symmetric Group and Noncrossing Partition
Friday, November 14, 2014, 2:30pm
Ungar Building Room 402
Abstract: The symmetric group Sn with its cycle notation and the idea of a Cayley graph will be discussed in the beginning. After that we will show two different generating sets for Sn. Based on this, we will define two important orders: weak order and absolute order. In the second half of the talk, we will introduce the idea of noncrossing partitions and prove a very important bijection between the maximal interval in absolute order of Sn and the noncrossing partition of n.
Armando Cabrera
University of Miami
will present
Some concepts in General Relativity
Friday, November 7, 2014, 2:30pm
Ungar Building Room 402
Abstract: In 1905 Albert Einstein proposed the theory that we call now Special Relativity. Although these new ideas described the consequences of the speed of light being constant, it did not include a gravitational theory. In 1916, Einstein proposed that the matter in the universe and its geometry are closely related. In this talk, we will describe the general idea of how this relation works and what type of mathematical objects are used in this field. As an example of the type of concepts/theorems in mathematical relativity, we will talk about the notion of total mass of a spacetime (ADM mass). Finally, we will obtain the total mass of the Schwazschild solution, which describes the gravitational field outside a spherical non-rotating massive body (a star or black hole).
Dr. Ken Baker
University of Miami
will present
Torus knots, cable spaces, and Dehn surgery
Friday, October 31, 2014, 2:30pm
Ungar Building Room 402
Abstract: We'll look at the complements of torus knots in S^3 and of torus knots in solid tori from a few different perspectives. Then we'll examine how to use these perspectives to create new classes of Dehn surgeries between these manifolds.
Yishu Song
University of Miami
will present
Self-Organized Criticality
Friday, October 24, 2014, 2:30pm
Ungar Building Room 402
Abstract: We'll discuss what self-organized criticality means with some real-world examples. To add mathematical flavor, we'll discuss a simple model of self-organized criticality, namely, the Bak-Sneppen model. Simple as this model may look, it is very difficult to prove rigorously results on its long-time behavior. Then we'll discuss some modified models and probable ideas and methods to analyze these models.
Brittney Ellzey
University of Miami
will present
What is Erhart Theory?
Friday, October 10, 2014, 2:30pm
Ungar Building Room 402
Abstract: Ehrhart theory gives a discrete analogy of volume by counting the number of integer points inside a polytope. The Ehrhart polynomial of a polytope gives the number of integer points inside dilations of the polytope. During this talk, I will introduce some of the basic concepts of Ehrhart theory and Ehrhart polynomials. I will work out a few examples in order for us to get a feel for the material, and I will also mention Pick's theorem, Stanley's nonnegativity theorem, and the Ehrhart-Macdonald reciprocity theorem.
Prayat Poudel
University of Miami
will present
What is...Gauge Theory?
Friday, October 3, 2014, 2:15pm
Ungar Building Room 402
Abstract: Gauge Theory has played an important role in the development of physics over the last century. The goal of this talk will be to provide an idea of what gauge theory is and why it is so important. We will mainly focus on its mathematical aspects while also discussing some of its applications in physics.
Jorge Cardona
University of Miami
will present
On Markov Chains
Friday, September 26, 2014, 2:30pm
Ungar Building Room 402
Abstract: We will discuss first time homogeneous Markov chains on a finite state space and the existence of invariant distributions given an ergodic transition matrix and we will connect this result with the Perron-Frobenius theorem. We will then move to the general case of a Markov Chain and discuss briefly the Doeblin and Strong Doeblin conditions to get an invariant measure and a representation of the state space on ergodic components and a transient set.
Alex Lazar
University of Miami
will present
The Tropical Picard Group
Friday, September 19, 2014, 4:30pm
Ungar Building Room 402
Abstract: A finite graph may be viewed as a combinatorial analogue of a one-dimensional algebraic variety. This analogy can be extended to higher-dimensional simplicial complexes. We give one example of this higher-dimensional analogy by defining a combinatorial invariant called the tropical Picard group of a simplicial complex. We then prove some basic results about the tropical Picard group for a particular class of simplicial complexes.
Christopher Langdon
University of Miami
will present
Hodge Numbers
Friday, September 12, 2014, 2:30pm
Ungar Building Room 402
Abstract: The Hodge numbers of a compact complex manifold are analytic invariants similar to the topologically invariant Betti numbers of a compact differentiable manifold. The Hodge numbers can be arranged into Hodge "Hodge Diamond" for the manifold and we will look at some of its symmetries. Furthermore, if the manifold is Kahler, we will see that these numbers can be viewed as a refinement of the Betti numbers of the underlying differentiable manifold.
Dr. Drew Armstrong
University of Miami
will present
Pascal's Mystic Hexagram
Friday, February 28, 2014, 2:30pm
Ungar Building Room 506
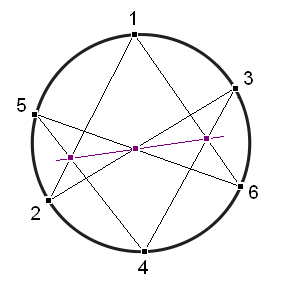
Abstract: When Blaise Pascal was 16 years old he published the following remarkable theorem. Consider any conic section in the plane (for example a circle). Choose any six points on the conic and connect them in any way as a hexagon (possibly self-intersecting). If you extend the three pairs of opposite sides of the hexagon they will meet at three collinear points (see the picture). I will explain the best way to prove Pascal's theorem. It involves complex numbers and points at infinity.
Kyle Evans
University of Miami
will present
Different viewpoints on SO(3)
Friday, February 21, 2014, 2:30pm
Ungar Building Room 506
Abstract: There are many ways to view SO(3) but in this talk i will focus on three. In an elementary manner i will show how the space of rigid rotations fixing the origin, RP(3) and the sphere bundled to the tangent space of the two sphere are all homeomorphic.
Armando Cabrera
University of Miami
will present
The Weyl Problem
Friday, February 14, 2014, 2:30pm
Ungar Building Room 506
Abstract: In 1916 Hermann Weyl described the following problem: Given a metric g with positive Gaussian curvature on the sphere S^2, is it realizable as a convex surface in R^3? If was not util 1953 when this problem was solved independently by Pogorelov and Nirenberg. In this talk we will go over the basic concepts of differential geometry to understand the Weyl problem and describe Nirenberg's proof.
Prayat Poudel
University of Miami
will present
SU(2) Representation Varieties of 3-Manifolds
Friday, February 7, 2014, 2:30pm
Ungar Building Room 506
Abstract: A powerful invariant of 3-manifolds is its Fundamental Group. However, this invariant can be very difficult to use. As an alternative invariant, we study homomorphisms of the Fundamental Group of 3-manifolds into SU(2). I will give a brief introduction to this topic.
Rafael S. González D'León
University of Miami
will present
The combinatorial structure behind multibracketed free Lie algebras
Friday, January 31, 2014, 2:30pm
Ungar Building Room 506
Abstract: We explore a beautiful interaction between algebra and combinatorics in the heart of the free Lie algebra on n generators: The multilinear component of the free Lie algebra Lie(n) is isomorphic as a representation of the symmetric group to the top cohomology of the poset of partitions of an n-set tensored with the sign representation. Then we can understand the algebraic object Lie(n) by applying poset theoretic techniques to the poset of partitions whose description is purely combinatorial. We will show how this relation generalizes further in order to study free Lie algebras with multiple compatible brackets. In particular we obtain combinatorial bases and compute the dimensions of these modules. Part of the talk is based on joint work with M. Wachs (UM).
Chris Langdon
University of Miami
will present
Visualizing Complex Functions Using Domain Coloring
Friday, December 6, 2013, 2:30pm
Ungar Building Room 402
Abstract: The graphs of complex valued functions of one complex variable are subsets of C^2 and so cannot be visualized directly. However, by using color and brightness to represent two of the real dimensions we can get a “picture” of the function. The aim of this talk will be to explain these pictures and use them to visualize the concepts of analytic continuation and Riemann surfaces.
Prayat Poudel
University of Miami
will present
Morse Theory and Handle Decomposition
Friday, November 22, 2013, 2:30pm
Ungar Building Room 402
Abstract: I will give a brief introduction to Morse functions and then use the idea of Morse function to show how a Morse function can be used to define a handlebody structure on a closed manifold.
Kyle Evans
University of Miami
will present
Group Cohomology and Group Extensions
Friday, November 8, 2013, 2:30pm
Ungar Building Room 402
Abstract: Group cohomology originates in topology but has a very interesting algebraic formulation in terms of group extensions with abelian kernels. I will discuss the classification problem for such extensions and use it to motivate the introduction of group cohomology.
Dr. Anton Dochtermann
University of Miami
will present
Topological data analysis
Friday, October 25, 2013, 4:00pm
Ungar Building Room 402
Abstract: These days everyone is talking about 'Big Data' (a Google search gives more than 30 million hits, and it even has its own Wiki page). Mathematically speaking we can think of Big Data as simply a large (but finite) collection of vectors in some high dimensional space. The assumption is that this data cloud is not just random, but in fact has some underlying (and 'hidden') structure. Perhaps the data is clumped into several components, or has high dimensional 'holes', or perhaps it even lies on some submanifold.
Topological data analysis, developed by Carlsson and collaborators, is a simple but powerful way to dynamically access this structure. The basic idea is to associate a one parameter family of topological spaces to the data cloud, and to record the Betti numbers (the 'holes') as we vary the parameter. The resulting 'bar code' tells us which features of the data 'persist', an insight into the 'shape' of the data. I will describe the basics of topological data analysis and sketch an application to the 'space of natural images'.
Dr. Kwok-Kun Kwong
University of Miami
will present
Hearing the shape of a drum
Friday, October 11, 2013, 2:30pm
Ungar Building Room 402
Abstract: In 1966, Mark Kac posed the famous question: Can one hear the shape of a drum? Physically, this is the question of determing the shape of a region (drum) given the list of all overtones (i.e. spectrum) it can make. It turns out that the answer is no. However, one can actually hear the dimension and the volume of a drum, thanks to Weyl's asymptotic formula. I will explain Kac's problem and verify Weyl's formula in a simple example.
Armando Cabrera
University of Miami
will present
The Isoperimetric Inequality and the Curve Shortening Flow
Friday, October 4, 2013, 2:30pm
Ungar Building Room 402
Abstract: One of the oldest theorems in Differential Geometry is the Isoperimetric Inequality, which is related to the Isoperimetric Problem: Of all simple closed curves in the plane with a given length L, which one bounds the largest area? This problem and its solution was known by the Greeks, but the first complete proof of the theorem did not appear until 1870. We will see how we can prove this theorem with elementary calculus. After this, we will introduce the Curve Shortening Flow and obtain the Isoperimetric Inequality from it.
Bridget Toomey
University of Miami
will present
Evaluating Phases and Orientations of Given Atomic Structures
Friday, September 27, 2013, 2:30pm
Ungar Building Room 402
Abstract: Rapid progress in material design has stimulated the need for development of new tools for efficient and accurate identification of new structure features and properties. This task is relatively straightforward in the case where the new materials are either purely crystalline or purely amorphous. However, these structures are generally new unknown polycrystalline structures that are hard to describe or identify, as they can be made of different regions characterized by different morphology, element types, and orientations. Since the crystal structures and orientations of these composites are vital in understanding and manipulating their properties, researchers require an accurate characterization of morphological properties at each region. However, no existing software can characterize polycrystals from the positions of their atoms.
Therefore, it is urgent to develop such tools. Our method rectifies this gap in crystallography research by designing an algorithm based on the lattice reduction approach (Krivy and Gruber 1976), which has been used in monocrystalline identification. We modify Krivy and Gruber's algorithm to accommodate polycrystalline and amorphous, non-crystalline structures.
Dr. Drew Armstrong
University of Miami
will present
What is ADE?
Friday, September 20, 2013, 2:30pm
Ungar Building Room 402
Abstract: Many deep classification problems in mathematics come down to the following: Find all triples of positive integers p,q,r such that 1/p+1/q+1/r is greater than 1. Exercise: What does this problem have to do with the attached diagram? In this talk I will explain the linear algebra phenomenon that underlies all such classifications. It is mysterious in a good way.

Dr. Shigui Ruan
University of Miami
will present
Modeling the Transmission Dynamics of Influenza
Friday, April 26, 2013, 3:45pm
Ungar Building Room 402
Abstract: Influenza viruses infect about 5 million people and cause about 500,000 deaths each year around the world, the reasons for the seasonal influenza epidemics are still not clear. There are two types of changes in influenza A viruses: antigenic drift which occurs all the time and causes the annual influenza epidemics and antigenic shift which happens only occasionally but causes pandemics. In this talk, we first present an age-structured type evolutionary epidemiological model of influenza A drift, in which the susceptible class is continually replenished because the pathogen changes genetically and immunologically from one epidemic to the next, causing previously immune hosts to become susceptible. Applying our recent established center manifold theory for semilinear equations with non-dense domain, we show that Hopf bifurcation occurs in the model. This demonstrates that the age-structured type evolutionary epidemiological model of influenza A drift has an intrinsic tendency to oscillate due to the evolutionary and/or immunological changes of the influenza viruses. We then introduce a model to describe the evolution of a "super-strain" of influenza (i.e., a strain composed of avian, human, and swine strains). By modeling the transmission dynamics of this super-strain between humans and pigs, we determine that the evolution of a super-strain is very likely and show that the transmissibility of a super-strain and the interaction between humans and pigs determine the epidemic outcome. The results emphasize the necessity of global surveillance of influenza activity in pigs to prevent future pandemics.
Armando Cabrera
University of Miami
will present
A discrete version of the Gauss-Bonnet theorem
Friday, April 19, 2013, 3:45pm
Ungar Building Room 402
Abstract: One of the deepest theorems in the differential geometry of surfaces is the Gauss-Bonnet theorem; it relates a geometric quantity, the Gaussian curvature, with a topological invariant, the Euler Characteristic. In this talk, we will review the definition of the Gaussian curvature of a smooth surface and define the corresponding concept for a (non-smooth) polyhedral surface. After this, we will be able to prove the Gauss-Bonnet theorem for such surfaces. This is closely related to Descartes' Elementary Treatise on Polyhedra, a work that remained unknown to the mathematical community for more than two hundred years.
Dr. Alexander Dvorsky
University of Miami
will present
Is exp(pi * sqrt (163)) odd or even?
Friday, April 12, 2013, 3:45pm
Ungar Building Room 402
Abstract: In fact, the number from the title is not an integer, but it is amazingly (up to twelve digits) close to being one, and the reasons for it are not so apparent. We will look deeper into this "coincidence", and will briefly discuss how different areas of mathematics (complex analysis, elliptic curves, number theory) are needed to fully understand it.
Blake Icabone
University of Miami
will present
The Poincaré-Hopf Theorem
Friday, April 5, 2013, 3:45pm
Ungar Building Room 402
Abstract: At any time, there is at least one point on the surface of the earth at which the wind is completely still. Why? We answer this question as we prove the Poincaré-Hopf theorem for surfaces, and recover a familiar topological invariant.
Andrew Sanchez
University of Miami
will present
Curvature, Areas and Volumes
Friday, March 29, 2013, 3:45pm
Ungar Building Room 402
Abstract: You have a goat on a 1 meter leash that you are setting out to graze. If you tie him up on a flat grassland, he will eat the right amount, if you tie him up at the top of a hill, he will starve, and if you tie him up in the middle of a valley, he will get fat. Why? We will first work out the details of surface area on 'hills', 'valleys', and 'grasslands', and then investigate the underlying geometric properties of these surfaces. Then we will generalize these notions to manifolds of arbitrary dimension, and discuss some results involving volume.
Rafael González D'León
University of Miami
will present
Introduction to graph coloring
Friday, March 8, 2013, 3:45pm
Ungar Building Room 402
Abstract: Imagine that you work in the UN, say in the International Court of Justice, and you are given the task to assign to each country in the world a lawyer of their preference to solve boundary disputes (two neighbor countries cannot share a lawyer). So you need to ask each country for a list of preferred candidates. What is the minimal length that you should require for these lists that would ensure you can make a proper selection? (If you think the answer is 4 maybe you need to analyze the problem a bit deeper).
Prayat Poudel
University of Miami
will present
Introduction to Dehn Surgery
Friday, March 1, 2013, 3:45pm
Ungar Building Room 402
Abstract: Dehn surgery is a basic method for constructing 3-manifolds. I will briefly describe the process as well as construct a few well-known 3-manifolds using Dehn surgery.
Dr. Anton Dochtermann
University of Miami
will present
Basics of Gröbner bases
Friday, February 22, 2013, 2:00pm
Ungar Building Room 402
Abstract: Fix an ideal I in a polynomial ring. A basic question in commutative algebra is to determine whether a given polynomial belongs to I. If the polynomial ring has just one variable, this is easy since all ideals are generated by a single element; we can use long division. In general, a `Gröbner basis' for I is a set of generators of I that have nice algorithmic properties. The construction of a Gröbner basis allows for a *multivariate* version of the division algorithm, as well as a *nonlinear* generalization of Gaussian elimination for solving systems of equations. We will discuss the basic notions of Gröbner bases and sketch the famous algorithm of Buchberger, which shows that a Gröbner basis can be obtained from any generating set of I. Time permitting we will mention some connections to polyhedral and tropical geometry.
Carlos Bajo
University of Miami
will present
Simplicial spanning trees
Friday, February 15, 2013, 2:00pm
Ungar Building Room 402
Abstract: Recently V. Krushkal and D. Renardy generalized the Tutte polynomial from graphs to cell complexes. We show that evaluating this polynomial at the origin gives the number of cellular spanning trees in the sense of A. Duval, C. Klivans, and J. Martin. Moreover, after a slight modification, the Tutte-Krushkal-Renardy polynomial evaluated at the origin gives a weighted count of cellular spanning trees, and therefore its free term can be calculated by the cellular matrix-tree theorem of Duval et al. In the case of cell decomposition of a sphere, this modified polynomial satisfies the same duality identity as before. We find that evaluating the Tutte-Krushkal-Renardy along a certain line is the Bott polynomial.
Dr. Marta Alpar Flothmann
University of Miami
will present
(Mostly) Basic Constructions of Category Theory
Friday, February 8, 2013, 3:45pm
Ungar Building Room 402
Abstract: First we'll look at some basic construction (limits, pullbacks, adjunctions) used in Category Theory and examples of these in other areas of mathematics. Then we'll examine the (not so basic) construction of a Topological Functor.
Matthias Leuenberger
University of Bern
will present
Automorphisms of C^n and Danielewski surfaces
Friday, February 1, 2013, 3:45pm
Ungar Building Room 402
Abstract: First I will present you some classical results about the structure of the algebraic and holomorphic automorphism group of C^n. If there is enough time we will see which of these results generalize to the class of surfaces {xy = p(z)} known as Danielewski surfaces.
Dr. Ken Baker
University of Miami
will present
Lens space surgeries, bandings of links, and DNA recombination
Friday, November 16, 2012, 3:45pm
Ungar Building Room 402
Abstract: Remarkably, aspects of molecular biology may be studied through low dimensional topology. In particular, we may interpret DNA recombination as particular types of transformations between knots and links which in turn may be analyzed through Dehn surgery on knots in 3-manifolds and corresponding 2-handle attachments to 4-manifolds. We'll focus on the middle ground demonstrating how the Montesinos trick relates these transformations between knots and links to Dehn surgery and then exhibit a conjectural classification of both biological and topological interest.
David Raps
University of Miami
will present
Triangles and Suicidal Clowns
Friday, November 9, 2012, 3:45pm
Ungar Building Room 402
Abstract: What do the trangulations of regular polygons and a clown on a cliff with a death wish have in common? This talk will be an introductory survey into Catalan numbers, a deep topic in combinatorics. We will examine many Catalan objects, their recursive properties and try to determine a closed formula.
Rafael S. González D'León
University of Miami
will present
About Algebras and Operads
Friday, November 2, 2012, 3:45pm
Ungar Building Room 402
Abstract: We will recall the definition of an algebra and discuss some familiar properties. We introduce then the notion of an operad and give a few examples.
Dr. Anton Dochtermann
University of Miami
will present
Links in embedded graphs
Friday, October 19, 2012, 3:45pm
Ungar Building Room 402
Abstract: We say that a graph G is "intrinsically linked" if no matter how G is realized in 3-space, we can find a pair of disjoint cycles that are linked. About 30 years ago Conway and Gordon (and independently Sachs) showed that K_6, the complete graph on six vertices, is intrinsically linked. Analogous to planarity of graphs, the property of "having a linkless embedding" is minor-closed and hence admits a finite family of "forbidden minors". In 1995 Robertson, Seymour, and Thomas proved a conjecture of Sachs giving a characterization of this family (there are 7 such graphs, including the Petersen graph). We will discuss Conway and Gordon's proof and survey some related results. Although I might mention some fancy techniques, most of the talk will be from first principles. And yes there is a similar (albeit less complete) story for "intrinsically knotted" graphs.
Dr. Drew Armstrong
University of Miami
will present
Plinko and the geometry of hypercubes
Friday, October 12, 2012, 3:45pm
Ungar Building Room 402
Abstract: The "Price is Right" game of "Plinko" was always my favorite. Remember "Plinko"? If not, click here. I recently discovered that this game is governed by the affine Cartan matrix of type C, which leads to an easy solution.
Eric Harper
McMaster University
will present
SU(N) Casson-Lin invariants for links
Friday, September 28, 2012, 3:45pm
Ungar Building Room 402
Abstract: We will introduce a family of invariants of links in the 3-sphere using projective SU(N) representations and braid theory. We will give some examples of computations, including the theorem that the SU(2) invariant of a two-component link is the linking number between its components.
Andrew Sanchez
University of Miami
will present
Markov Chains
Friday, September 21, 2012, 3:45pm
Ungar Building Room 402
Abstract: Markov Chains are a useful way of modeling random processes that transition between a finite number of states. In this talk we will start with the formal definition of a Markov Chain and some basic definitions, and then derive some results regarding Markov Chains with absorbing states. Time permitting, we will discuss some applications such as the Gambler's Ruin.
Armando Cabrera
University of Miami
will present
The Zeeman Topology on the Minkowski Spacetime
Friday, September 14, 2012, 3:45pm
Ungar Building Room 402
Abstract: The Minkowski Spacetime, which is R^4 eqquiped with a metric of signature 1, is the model of the Special Relativity. In this space we can define a partial order relation, x<y, when y is in the chronological future of x. It was proven by E.C. Zeeman that this relation is preserved by causal automorphisms (i.e., orthochronus Lorentz tranformations, translations and dilatations). However, as the usual topology on R^4 does not distinguish between timelike, lightlike and spacelike directions, it admits continuous functions that have no clear physical meaning, i.e., the previous relation is not preserved. In this talk we will define the Zeeman topology on the Minkowski Space and extract some important properties. This topology has the nice feature that the homeomorphisms are generated by Lorentz group, translations and dilatations; a brief description of the proof of this fact will be given.
Prayat Poudel
University of Miami
will present
Introduction to knot theory
Friday, September 7, 2012, 3:45pm
Ungar Building Room 402
Abstract: A knot can be thought of as a continuous loop in three dimensional space made up of a thin elastic rubber band. Given two knots we would like to be able to determine if one can be deformed into the other without cutting or pasting. In this talk, I would like to give a few basic definitions and then introduce various techniques which will allow us to distinguish knots.
Xiaocong Deng
University of Miami
will present
De Rham's theorem
Friday, April 27, 2012, 4:00pm
Ungar Building Room 402
Abstract: De Rham cohomology is a cohomology theory of smooth manifolds based on differential forms. It relates analysis on a manifold to its topology via the de Rham theorem which establishes an isomorphism between the de Rham and singular cohomology. The proof of this theorem that we will talk about will rely on the Mayer--Vietoris sequences and the Whitney approximation theory.
Yijia Liu
University of Miami
will present
Almost Complex Structures
Friday, April 20, 2012, 4:00pm
Ungar Building Room 402
Abstract: The existence of a complex structure has a central role in many physical problems. But sometimes it can be quite difficult to determine whether a manifold admits a complex structure. An example in this respect is the six dimensional sphere \(S^6\). In this talk, I will introduce the notion of almost complex structure and its relation to complex structure. An interesting result is that the only almost complex spheres are \(S^2\) and \(S^6\). I will give a criteria (Wu's Theorem) for 4-manifolds and show that \(S^4\) does not admit an almost complex structure.
Christopher Smith
University of Miami
will present
Exotic 7-spheres
Friday, April 13, 2012, 4:00pm
Ungar Building Room 402
Abstract: In this talk I will explain the notion of exotic manifolds, and give an example of an exotic 7-dimensional sphere, using fiber bundles, morse theory and the hürzebruch signature theorem to show it is homeomorphic but not diffeomorphic to the standard 7-dimensional sphere.
David Harden
University of Miami
will present
Spin Groups
Friday, April 6, 2012, 4:00pm
Ungar Building Room 402
Abstract: In this talk, we are going to look at the representation theory of the Clifford algebra \(Cl(\mathbb{R}^n)\), the spin group \(Spin(n)\), and a group of order \(2^{n+1}\).
Dr. Daniel A. Díaz Pachón
University of Miami
will present
Allocations: what they are and some open problems
Friday, March 30, 2012, 4:00pm
Ungar Building Room 402
Abstract: Point processes are a probabilistic tool used in several fields of science (astronomy, particle motion, survival analysis, etc.) When analyzing (stationary) point processes, it is often useful to do it from the perspective of a "typical" point in the process. Although it is easy to do when there are finitely many points (one is chosen uniformly at random), the selection is very difficult when there are infinitely many points to be considered. In order to do so, we usually take the Palm version of the point process Z —i.e., a process Z' with the same law of Z conditioned to have a point in the origin— to select the origin as "typical". Allocations provide a way to translate Z in such a way that the translated process will have the law of Z'. In this talk, we analyze several of these allocations, their interesting graphical representations and some open problems.
Prayat Poudel
University of Miami
will present
Yang-Mills Theory and the Maxwell Equations
Friday, March 23, 2012, 4:00pm
Ungar Building Room 402
Abstract: In this talk I will introduce the Yang-Mills equations and convey the basic idea behind the equations. I will also show that Maxwell's equations are a particular case of the Yang-Mills equations.
Dr. Nikolai Saveliev
University of Miami
will present
The Triangulation Conjecture
Friday, March 02, 2012, 4:00pm
Ungar Building Room 402
Abstract: One of the oldest and most difficult problems in manifold topology is the triangulation conjecture which states that every topological manifold is homeomorphic to a simplicial complex. The conjecture is known to be true in all dimensions up to three, false in dimension four, and it remains open in dimensions five and higher. I will outline the progress to date and will explain how gauge theories of theoretical physics have emerged as a major tool in dealing with the conjecture.
Kyle Evans
University of Miami
will present
Division Algebras
Friday, February 24, 2012, 4:00pm
Ungar Building Room 402
Abstract: We will prove that in order for a real vector space to be a division algebra, that is, to admit a bilinear product operation without zero divisors, its dimension must be a power of two. The proof will use the Stiefel-Whitney class.
Rafael S. González D'León
University of Miami
will present
A Cell Structure for Grassmann Manifolds
Friday, February 17, 2012, 4:00pm
Ungar Building Room 402
Abstract: We are going to follow an exposition due to J.W. Milnor of a canonical cell decomposition of the Grassmann manifold due to C. Ehresmann. The main idea is to show that the Grassmannian can be provided with the structure of a CW-complex, how the cells are constructed and give a few examples.
Armando Cabrera
University of Miami
will present
Special Relativity from an intuitive viewpoint through Spacetime Diagrams
Friday, February 10, 2012, 4:00pm
Ungar Building Room 402
Abstract: In 1905, Albert Einstein published a new theory that in our days is known as Special Relativity. This theory is based in two fundamental postulates:
1) The laws of Physics are the same for any inertial observer.
2) The speed of light is constant.
Usually, if we take a class of Special Relativity, it will begin with the explanation of the most important phenomena implied by the postulates and the instructor will infer those phenomena after introducing the Lorentz Vector Spaces (i.e. scalar product vector spaces of signature 1 of dimension greater than 1). In this talk, based on the work of Hermann Bondi (1962), I will derive the most popular features of Special Relativity, e.g. the time dilatation, the relativistic addition of velocities and the space contraction, from an intuitive viewpoint (without the necessity of Lorentz Transformations) through the so called Spacetime Diagrams. I hope that after this talk, as Bondi would have liked, the words Relativity and Common Sense won't be unrelated anymore.
Dr. Anton Dochtermann
University of Miami
will present
Topology of colorings and graph homomorphisms
Friday, February 3, 2012, 2:15pm
Ungar Building Room 402
Abstract: A 'proper coloring' of a graph G is an assignment of colors to the vertices of G such that adjacent vertices receive different colors (a special case of a more general notion of 'graph homomorphism'). The chromatic number of a graph G is the smallest number of colors needed to properly color G. Proving upper bounds on chromatic number is some sense easy (just exhibit a coloring) but in general lower bounds are hard to come by. In the 70s Lovasz studied a class of graphs defined in terms of intersecting subsets (known as 'Kneser graphs') and established a lower bound on their chromatic number (matching upper bounds were already known). His proof was surprising in that it employed basic notions of algebraic topology along the lines of the Borsuk-Ulam Theorem, and ushered in techniques which now come under the heading of 'topological combinatorics'. We'll discuss Lovasz's proof in the context of more contemporary 'homomorphism complexes' of graphs, and discuss extensions and the general theory that has emerged. In keeping with the theme of the seminar we'll at least mention Stiefel manifolds and characteristic classes.
Armando Cabrera
University of Miami
will present
An introduction to Lagrangian Coherent Structures
Friday, November 18, 2011, 4:00pm
Ungar Building Room 402
Abstract: Early in the morning we drink our first cup of coffee of the day. We add to our coffee some cream (at least some of us), after a few seconds (if we don't mix it), some funny shapes start to form. Why does the cream in our coffee have these patterns? Can we understand them? Perhaps our cream doesn't move as freely as we thought. These questions lead us to the study of transport in chaotic fluids (yes, our morning coffee is chaotic). In this talk I will give a very intuitive introduction to how these "structures", known as Lagrangian Coherent Structures (LCSs), are understood through math. It will include some differential geometry combined with dynamical systems. I will motivate their study with applications they have to oceans' dynamics modeling and I hope this will give you an idea of why I consider this an interesting problem.
Carlos Vega
University of Miami
will present
The Gromov-Hausdorff Topology: Taking Limits of Riemannian Manifolds
Friday, November 11, 2011, 4:00pm
Ungar Building Room 402
Abstract: It is a natural question, which arises in practice, to ask how one might take the limit of a sequence of Riemannian manifolds. Several notions of convergence have been developed, but we will focus on the Gromov-Hausdorff topology. After a brief motivation, including that of the Ricci flow, we will focus on getting a feel for the Gromov-Hausdorff distance by working out some basic examples and results. Time permitting, we will discuss alternative notions of convergence and the pros and cons of each.
Daozhou Gao
University of Miami
will present
A survey of three-dimensional competitive Lotka-Volterra systems
Friday, November 04, 2011, 4:00pm
Ungar Building Room 402
Abstract: In this talk, I will review some advances up to most recently on three-dimensional competitive Lotka-Volterra systems. Selected topics may include the limit sets, the number of limit cycles, the properties of the carrying simplex, the model with reaction-diffusion term, discrete May-Leonard models and some applications.
Dr. Shulim Kaliman
University of Miami
will present
Algebraic automorphisms of Euclidean spaces.
Friday, October 28, 2011, 4:00pm
Ungar Building Room 402
Abstract: We discuss the notion of an algebraic automorphism of a Euclidean space (that is also called a polynomial coordinate substitution). We consider properties of the group of such automorphisms, its one-dimensional unipotent subgroups, and the actions generated by these subgroups on Euclidean spaces. Some nontrivial results and problems associated with these notions will be discussed.
Dr. Gabriel Kerr
University of Miami
will present
A gentle introduction to mirror symmetry
Friday, October 21, 2011, 4:00pm
Ungar Building Room 402
Abstract: In this talk I will discuss the origins and basic ideas of mirror symmetry. This subject now involves an extremely wide range of mathematics and physics topics, among which are conformal field theories, D-branes, enumerative geometry, complex algebraic geometry, symplectic geometry, combinatorics, derived categories and even number theory. By way of examples, I will explain how the above subjects are related to mirror symmetry.
Prayat Poudel
University of Miami
will present
Introduction to Vector Bundles
Friday, October 7, 2011, 4:00pm
Ungar Building Room 402
Abstract: In this talk I plan to give a brief introduction to vector bundles along with motivation for the study of vector bundles. If we have time, I will also talk about the geometry of vector bundles.
Christopher Harris
University of Miami
will present
Some Infinite Dimensional Groups and Algebras
Friday, September 30, 2011, 4:00pm
Ungar Building Room 402
Abstract: After briefly reviewing the notions of Lie groups and Lie algebras we will introduce the idea of a loop group. These are also Lie groups since they have a group structure and the structure of infinite-dimensional manifolds. We will then discuss their Lie algebras, loop algebras, and construct their central extensions which are known as (untwisted) affine Lie algebras. If we have time, we will also discuss the diffeomorphism group of the circle and the Virasoro algebra. All of these notions are essential in many parts of physics, especially string theory.
Dr. Drew Armstrong
University of Miami
will present
What is... a Root System?
Friday, September 23, 2011, 4:00pm
Ungar Building Room 402
Abstract: Fact 1: Every isometry \(\varphi:\mathbb{R}^n\to\mathbb{R}^n\) is affine. That is, we can write \(\varphi(x)=Ax+b\) for some matrix \(A\) and vector \(b\). Fact 2: (Cartan-Dieudonné) Every othogonal matrix \(A\in O(n)\) is the product of at most \(n\) reflections. Conclusion 1: The study of euclidean geometry is the study of the orthogonal group \(O(n)\). Conclusion 2: The orthogonal group is generated by (infinitely many) reflections. Question 1: What can be said about groups generated by finitely many reflections? Answer 1: Quite a lot, actually.
Dr. Ken Baker
University of Miami
will present
An Introduction to Representations of \(sl_2(\mathbb{C})\)
Friday, September 16, 2011, 4:00pm
Ungar Building Room 402
Abstract: Representations of \(sl_2(\mathbb{C})\) are fundamental in the study of Topological Quantum field Theory. We'll introduce Lie algebras and their representations with a focus on the Lie algebra \(sl_2(\mathbb{C})\). This is the first talk in a working seminar on TQFTs, following the course notes by Ko Honda available at http://www-bcf.usc.edu/~khonda/math635/notes.pdf
Rafael S. González D'León
University of Miami
will present
What is... a Matroid?
Friday, September 09, 2011, 4:00pm
Ungar Building Room 402
Abstract: A concept introduced by H. Whitney in the 30's. A matroid is a rich combinatorial structure that arises naturally in vector spaces, graphs, field extensions, stable polynomials, etc... It has a great variety of descriptions and applications. We will discuss the definition and some notions and examples that motivate the theory.
Matthew Hyatt
University of Miami
will present
On the Littlewood-Richardson Rule
Friday, April 15, 2011, 2:30pm
Ungar Building Room 506
Abstract: This talk will begin with the definition of a group representation, and end with the famous Littlewood-Richardson rule, covering the necessary results in between. The Littlewood-Richardson rule is a combinatorial description of certain important coefficients that arise in the study of symmetric functions (these are the coefficents that give the expansion of a product of Schur symmetric functions in terms of the Schur basis). These coefficients also arise in the study of representations of the symmetric group (how to decompose the induced representation of a tensor product into irreducible representations), as well as other places. In the process of this talk, we will also have the chance to observe instances of interactions between representation theory and combinatorics.
Liz Jimenez
University of Miami
will present
Enumerating faces of Zonohedra
Friday, April 8, 2011, 2:30pm
Ungar Building Room 506
Abstract: A zonohedron is a 3-dimensional convex polytope defined as the Minkowski sum of line segments. A way to better understand zonohedra is to enumerate their faces and the incidences between the faces, in other words, to study their flag f-vector.
It has long been known that there is a duality between the nonempty faces of a zonohedron Z and the faces of the hyperplane arrangement whose fan is the same as the normal fan of Z. We define a family of 3-dimensional hyperplane arrangements and characterize the flag f-vectors of those arrangements. Then, we translate the results to the dual setting of zonohedra.
Daniel Ryan
University of Miami
will present
Alignment of DNA Sequences
Friday, March 25, 2011, 2:30pm
Ungar Building Room 506
Abstract: Alignment of two strings refers to performing the operations of inserting, deleting and substituting the characters of one string to turn it into the other. Measuring the number and types of operations needed to align two strings can give an idea of the similarity between the strings.
Alignment of DNA sequences (strings composed of A’s, C’s, G’s and T’s) is an extraordinarily common task in modern biology. In this talk, I will describe the dynamic programming algorithms used to solve this alignment problem as well as the faster BLAST heuristic that has been developed to search large DNA sequence databases. The BLAST algorithm first appeared in the 1990’s and just two papers about this algorithm combine for a whopping 68,000 citations!
Julian Moorehead
University of Miami
will present
Partial Set Partition Lattices
Friday, March 11, 2011, 2:30pm
Ungar Building Room 506
Abstract: In the study of partially ordered sets, the class of finite geometric lattices forms an important family with similar topological results. In this talk, I will discuss geometric lattices, followed by a construction which can be placed on these objects to form a related set of objects called partial set partition lattices, as well as some results which may then be extracted from this.
Daozhou Gao
University of Miami
will present
A Brief Introduction to Epidemic Patch Models
Friday, March 4, 2011, 2:30pm
Ungar Building Room 506
Abstract: Epidemic patch models are useful for studying the effects of population dispersal on the spatial spread of infectious disease between different areas. In this talk, I will start with the topics of patch models and epidemic models, then their combination-epidemic patch models. Finally, I will discuss my recent work on an SIS epidemic patch model.
Carlos Vega
University of Miami
will present
Walkable Spacetimes
Friday, February 25, 2011, 2:30pm
Ungar Building Room 506
Abstract: As you read this abstract, a dragon is stealing your baby! He will leave a note saying where to meet him tomorrow to exchange the child for a, very reasonable, ransom of $5. After panhandling for the rest of the evening, you will raise the necessary funds and arrive at the meeting place the next day to find the dragon waiting for you with baby in hand. You will take a step towards the dragon, but something strange will happen; The distance between you will increase! You'll take another step towards him but will end up farther still! You will run towards the dragon at full speed only to see him shrink away into the horizon, along with the child you will never see again. ... Space does change size and shape over time; COULD THIS HAPPEN TO *YOUR* BABY???!!! (... Is spacetime 'walkable'?)
Prayat Poudel
University of Miami
will present
What is... Morse Theory?
Friday, February 18, 2011, 2:30pm
Ungar Building Room 506
Abstract: The beauty of Morse theory lies in the fact that it gives us tools to study the topology of manifolds using the critical points of special functions (called Morse functions) defined on the manifold. In this talk I will give a brief introduction to the subject as well present some interesting applications.
Christopher Harris
University of Miami
will present
(CANCELLED)What is... a Modular Form?(Part II)
Friday, February 11, 2011, 2:30pm
Ungar Building Room 506
Abstract: The talk is a continuation of the previous talk where we are going to discuss some examples and we will also describe the structure of modular forms as a graded ring.
Christopher Harris
University of Miami
will present
What is... a Modular Form?
Friday, February 4, 2011, 2:30pm
Ungar Building Room 402
Abstract: At first sight the definition of a modular form is quite opaque. We will provide context for this definition by discussing lattices in the complex plane and how modular forms can be viewed as certain "functions" on the moduli space of elliptic curves. We will also describe the structure of modular forms as a graded ring.
David Harden
University of Miami
will present
The Leech Lattice
Friday, November 19, 2010, 2:30pm
Ungar Building Room 402
Abstract: I plan to cover what the Leech lattice is, what its symmetry group Co_0 looks like, and, depending on time, one or more of the strange groups that can be found within Co_0 as subquotients.
Carlos Vega
University of Miami
will present
Spacetime, Singularities, and the Bartnik Conjecture
Friday, November 12, 2010, 2:30pm
Ungar Building Room 402
Abstract: In 1916, Schwarzchild produced the first meaningful solution to general relativity, a spacetime modeling the simplest universe imaginable: a single star at rest in an otherwise empty void. He soon discovered, however, that his solution came with an interesting and tragic emotional defect: at the heart of the loneliest star in the world, lay a tiny, Irreparable 'hole' or 'singularity'.
In fact, singularities of this kind continued to crop up in other spacetime solutions and their significance remained rather unclear until 1970, when Hawking and Penrose finally put the question to rest. (Their conclusion? ... You'll have to wait and find out!)
Hawking and Penrose's singularity theorems depend on *strict* curvature inequalities. The associated rigidity question remains open and is known as the Bartnik Conjecture. In this talk, we will introduce spacetimes, singularities, and a precise statement of this conjecture. If time permits, we will then solve the conjecture.
Armando Cabrera
University of Miami
will present
Mathematical Relativity and a compactification of the Minkowski Spacetime
Friday, November 5, 2010, 2:30pm
Ungar Building Room 402
Abstract: In this talk we will go through the basic definitions of mathematical Relativity. After this brief introduction, we will focus our attention on the Minkowski Spacetime. We will talk about the transformations that preserve separation zero (i.e. when a signal of light can pass between two events). In order to extend this kind of transformations when they are defined in proper subsets of the Minkowski Spacetime, we will have to join to this spacetime a "null cone at infinity". The result is a compact space which is called the Conformal Minkowski Spacetime (Lester, J. and Popovici et al). The aim of the talk is to construct this space, if we have some time left, I'll give a sketch of the proof of the theorem of characterization of such transformations.
Matthew Hyatt
University of Miami
will present
Double Feature
Friday, October 29, 2010, 2:30pm
Ungar Building Room 402
Abstract: The first part of the talk will be a review of a connection between representation theory and symmetric functions. In the second part we consider a colored analog of Eulerian quasisymmetric functions. Eulerian quasisymmetric functions were introduced by Shareshian and Wachs in order to obtain a $q$-analog of Euler's exponential generating function formula for the Eulerian numbers. They are defined via the symmetric group, and applying the stable and nonstable principal specializations yields formulas for joint distributions of permutation statistics. We consider the group of colored permutations and use this group to introduce colored Eulerian quasisymmetric functions. We derive a formula for the generating function of these colored Eulerian quasisymmetric functions, and show that applying the stable and nonstable principal specializations yields formulas for joint distributions of colored permutation statistics, generalizing Euler's formula.
Kyle Evans
University of Miami
will present
Markov chains and a few thought experiments
Friday, October 22, 2010, 2:30pm
Ungar Building Room 402
Abstract: Markov chains are a well known and very simple modeling tool. I will briefly go over some interesting results and applications and theory. This talk will focus on discrete chains and consider a few applications to game theory including Parrondo's "paradox".
Julian Moorehead
University of Miami
will present
A Brief Survey of Posets and Their Topology
Friday, October 8, 2010, 2:30pm
Ungar Building Room 402
Abstract: Everyone is familiar with partial orderings of different types, from the classical ordering of numbers to other, more interesting orders on different sets. But we can also analyze these partial orders in more abstract ways, including homological techniques, which provide interesting insights into their structures. This talk will briefly examine some of these techniques and how they can be used.
Douglas Schieb
University of Miami
will present
A Survey of Mathematical Models of Biological Systems
Friday, October 1, 2010, 2:30pm
Ungar Building Room 402
Abstract: It is well known that mathematics can be used to understand physical systems. But it is less well known that mathematics can be used to understand biological systems. My aim in this talk is to give a non-technical survey of mathematical models which are used to study various biological systems and describe how slight changes in the biological assumptions are incorporated into these models. I will primarily focus on population models, which will lead into my research, and will also briefly discuss epidemiological and physiological models.
Rafael S. González D'León
University of Miami
will present
About the Potts model and some of its combinatorial relations
Friday, September 17, 2010, 2:30pm
Ungar Building Room 402
Abstract: I will be discussing how the Potts model is defined in statistical mechanics and some combinatorial relations derived from its definition. The talk aims to be essentially combinatorial but will borrow some terminology from fundamental concepts in physics. The discussion in this talk is due to Alan D. Sokal and can be found in his paper.
Christopher Harris
University of Miami
will present
Geometry in Classical Mechanics
Friday, September 10, 2010, 2:30pm
Ungar Building Room 411
Abstract: My aim is to introduce some of the ideas one learns as an undergraduate physics major in the language one learns as a graduate student in math. We will make use of both perspectives to become familiar with the rigorous as well as the heuristic aspects. We begin by deriving the Euler-Lagrange equations. Then we will make the passage from Lagrangian to Hamiltonian Mechanics and describe how the equations of motion can be expressed naturally using the symplectic structure of phase space.





